Airy on Pendulums and Balance Wheels

A transcription of: Airy, George Biddell. "On the Disturbances of Pendulums and Balances, and on the Theory of Escapements." Transactions of the Cambridge Philosophical Society Vol. III, Part I (1830): 105-128, Plate 2.

III¹ On the Disturbances of Pendulums and Balances,
and on the Theory of Escapements.

PLUMIAN PROFESSOR OF ASTRONOMY AND EXPERIMENTAL PHILOSOPHY, FELLOW OF TRINITY COLLEGE, AND OF THE CAMBRIDGE PHILOSOPHICAL SOCIETY.

HAVING lately had occasion to investigate the disturbance produced in the motion of a pendulum by a small external force, and having found by a very general investigation a result of great simplicity, I perceived that the usual theorems for the alteration in the time and extent of vibration produced by the difference between cycloidal and circular arcs, by the resistance of the air, by the friction at the point of suspension, &c. could be made to depend on it; and that these alterations could in fact be found with greater facility from this general theorem than from the independent and unconnected investigations. I found also that the same principles could be applied with great ease to that important practical subject, the escapements of clocks - a subject upon which I believe no distinct theory has ever yet been laid down. The investigations which have been the fruit of these considerations are now presented to the notice of this Society: the theory of escapements is by no means complete, but I hope it will be found that the principal points have been touched on, and that enough is said to enable any one else to pursue the subject as far as he may wish.

If l be the length of a pendulum vibrating in a cycloidal arc, x its distance at any instant from the position of rest, the equation of its motion is

a and b being constants depending on the length of the arc and the time of passing the lowest position. The velocity at any time

Suppose now that, besides the force which varies as the distance, another very small accelerating force f acts on the ball of the pendulum in the direction in which x is measured positive:

The solution of this equation may still be assumed

, provided we consider a and b as functions of t. For whatever the solution may be,

, may be made equal to it by assuming either for a or for b a proper form. Since then a single assumption will satisfy this condition, and since we have two quantities whose forms are to be determined, it follows that we are at liberty to make another assumption. Let this be that the velocity shall be expressed by the same form as before, namely,

. The convenience of this assumption we shall soon discover.

If we could solve these two differential equations, we should have the complete determination of the motion.

In few cases, however, it is practicable to obtain an exact solution: and in all an approximation is sufficient for our purposes. This may be obtained by integrating the expressions

on the supposition that a and b are constant. As a and b are variable, this process is erroneous. But as their variation depends on f, the error depends on f ², or on quantities of that order. Our approximation then will include all terms depending on the first power of f, and no more: an approximation sufficiently exact for all the cases to which we shall have to apply it.

Since the expression for the distance of the pendulum from its lowest position, and the expression for the velocity of the pendulum, are the same as those in an undisturbed cycloidal pendulum where a is the extent of the vibration, on each side, and b / n the time which elapsed from the instant at which the pendulum passed its lowest position to the instant from which t is measured, it is plain that if the disturbing force ceased, the pendulum would move in the same manner: that is, the extent of its vibration would be a, and it would move as if it had passed its lowest point at the time - b / n a and b having the values which they had at the instant when the force ceased to act. And generally, considering a and b as functions of t, the time of arriving at the lowest point will be determined by making

In order to find the alteration in the length of the arc of vibration which takes place in one oscillation, we must integrate

through the limits of t corresponding to one oscillation; that is, from a value of t which gives

, to the value of t, which gives

. Here a may be any thing

that we please: in some cases it will be convenient to take the integral from one extremity of the vibration to the other: in others it will be preferable to take it from the time at which the pendulum passes its lowest position to the time at which it again arrives there. In some cases it will be necessary to integrate for two vibrations.

To find the alteration in the length of time occupied by a vibration, produced in one oscillation, let B be the value of b at the first limit, and B' that at the second: and let T and T' be the times. Then the first time at which the pendulum passes its lowest point is found by making

: the second time is found by making

. Hence

between the proper limits. Consequently the time of oscillation is increased from

If the circumstances were such that it was necessary to integrate through two vibrations, we should have

These formulæ are convenient when the disturbing forces can be expressed in terms of t. If, however, they are expressed in terms of x (as is the case particularly in clock escapements),

EXAMPLE 1. Instead of vibrating in a cycloid, the pendulum vibrates in a circle. Here the force

EX. 2. The friction at the point of suspension is constant. Here

; and it will be convenient to take the integrals during that time in which the friction acts in the same direction, that is, from the beginning of a vibration to its end, or from

EX 3. The resistance varies as the m ^th power of the velocity, or

, m being any whole number.

EX. 4. The resistance is expressed by any function of the velocity. Here

, and the increase of the arc

the integral being taken from

again. But it must be observed that from

, the radical must be taken with a negative sign, because

is then negative. The increase of the arc is, therefore, the sum of

This taken between the limits

is in all cases = 0. A resistance, therefore, which is constant, or which depends on the velocity, does not alter the time of vibration.

EX. 5. The resistance is that produced by a current of air moving in the plane of vibration with a velocity V greater than the greatest velocity of the pendulum; and varies as the square of their relative velocity. In this case, when the pendulum moves in the direction of the current

By the formula above we find that when the pendulum moves in the direction of the current, the arc is increased by

The diminution in two vibrations is, therefore,

. The time of vibration is unaltered.

EX. 6. The resistance is that produced by a current of air whose velocity is not equal to the greatest velocity of the pendulum. Here, when the pendulum moves in the direction of the current

when

, and

when

. By the formula above, the increase of the arc is

The time is not altered. The motion in the opposite direction is the same as in the last Example.

EX. 7. The force F acts through a very small space s at the distance c from the lowest point. For the increase of the arc we must take

if the general value of the integral be

, the value between these limits will be

nearly

If then an impulse be given when the pendulum is at its lowest point, c is 0, and the time of vibration is unaffected.

A force f which is equal at equal distances from the lowest point on both sides accelerates the pendulum. By the general formulæ it will be found that the action on both sides of the lowest point tends to increase the arc; but that the action, before reaching the lowest point tends to diminish the time of oscillation, and that after it to increase the time, and that on the whole the time of oscillation is not altered.

A force M which is equal at equal distances retards the pendulum as it ascends from the distance c to its highest point, and accelerates it as it descends to the same place. Upon taking

from

till

again

, we find that the length of the arc is not altered. In rising the time of vibration is increased by

To find the effect produced as the pendulum descends we must remark that

was introduced as equal to

, which then becomes negative; and the radical must therefore be taken with a negative sign. We must, therefore, take

A force of this kind then does not alter the arc of vibration, but tends during the whole of its action to diminish the time.

Since the theory is applicable to every case in which a pendulum is acted on by small forces, it can be applied to determine the effect produced on the motion of the pendulum of a clock, or the balance of a watch, by the machinery which serves to maintain that motion. After describing generally the manner in which the weight by the intermediation of the wheel-work acts on the pendulum, and stating the principles to be observed in the construction of escapements which follow from the investigations above, we shall proceed to examine the escapements which are most in use.

If a pendulum vibrates uninfluenced by any external forces except that of gravity, the resistance of the air and the friction at the point of suspension reduce gradually the extent of vibration. But this diminution goes on very slowly. I have observed a pendulum suspended on knife edges vibrate more than seven hours before its arc was reduced from two degrees to 1/5th of a degree. In order to maintain vibrations of the same or nearly the same length (which for clocks is indispensible) a force must act on the pendulum: this force is generally given by the action of the tooth of the seconds wheel on the inclined surfaces small arms or pallets carried by the penduIum: and the whole apparatas is called the escapement. It is necessary, therefore, in the theory of escapements, to consider the motion of the pendulum when, besides the force arising from its own weight, it is acted upon by the resistance of the air, &c. and by the force impressed by the machinery. The fact stated above shows that the first of these forces, and consequently the second, are so small that our approximate theory is abundantly sufficient for this investigation.

Now it appears from Examples 2, 3, 4, 5, and 6, that the friction and the resistance of the air do not affect the time of vibration. The maintaining force, therefore, must be impressed

in such a manner as not to alter the time of vibration. With this construction a compensated pendulum moving in a cycloidal arc would be isochronous. But the pendulums of clocks swing in circular arcs, and it might therefore appear desirable to make the escapement in such a manner as to correct the difference between the circular and the cycloidal vibration. In this manner, the oscillations would always be isochronous, whatever variations the maintaining power and the length of the arc of oscillation might undergo.

Upon a more accurate examination, however, I believe it will be found much better to lay aside all thoughts of this artifice. The law of the air's resistance when the velocity is so small as that of a pendulum is not known. By observations on detached pendulums of Captain Kater's construction, I have found that it differs very much from that of the square of the velocity. Whether it would be better represented by the simple velocity or by the square of the velocity increased by a constant, I do not know. Besides this, it is almost impossible to ascertain the effect of the friction upon the pallets, or its proportion to the resistance to the air, &c. Since then we cannot express, in a known function of the length of the arc, the diminution of the arc at each vibration, or the quantity which the maintaining force must increase it at each vibration, we cannot find what the force must be to maintain a given extent of vibration, and, therefore we cannot find in what manner it must be applied that its effect on the time of vibration may exactly counteract that of the difference between the circular and cycloidal arcs. It is possible also in pendulums with a spring suspension, to make the vibrations very nearly isochronous in different arcs; and in pendulums with knife edge suspensions, it is easy to apply a construction which will have the same effect. I shall, therefore, consider it as the object in the construction of escapements to make them in such a manner that they do not at all affect the time of vibration.

The escapements of clocks in general use may be divided into the three following classes: recoil escapements, dead-beat escapements: and the escapements in which the action of the wheels raises a small weight which by its descent accelerates the pendulum. The last may be called, from the name of their first proposer, Cumming's escapements.

I shall first observe that the friction which in the recoil and dead-beat escapements takes place during the whole vibration does not appear to affect the time of vibration. This friction may be separated into two parts: that which is properly called friction, arising from the rubbing of two bodies, and that which arises from the viscidity of the oil. The former of these is generally considered to be constant, and the latter to vary nearly as the velocity. Consequently, by Examples 2 and 3, they do not alter the time of oscillation. It is undoubtedly important that friction should be avoided if possible, as a smaller maintaining power is then required, and the irregularities which it may occasion in the pendulum's motion are proportionally diminished. In the dead-beat escapement this friction is interrupted during the time in which the wheel is acting on the pallets. We may, however, suppose a retarding force to act during this time, provided we add to the maintaining power an equal force. In Cumming's escapement the friction is nothing.

In the recoil escapement, soon after the pendulum has passed its lowest position a force begins to retard it till it reaches the extremity of its vibration: then (acting still in the same direction) it accelerates it till it has again passed the lowest point by the same distance as before: then another retarding force commences its action, &c. We may then consider the action of the force as divided into two parts, of which one retards the ascent of the pendulum and accelerates its descent, and the other accelerates the pendulum a little before and a little after it has reached its lowest point. The former of these, by Example 9, has no effect

at all in maintaining the arc of vibration, but always diminishes the time. The latter, by Example 8, if it be equal on both sides of the lowest point has no effect on the time of vibration, but increases the arc of vibration if there be no resistance, or maintains it if there be resistance. The former of these, then, is of no use whatever, and is prejudicial as affecting the rate of the clock: the latter does not affect the rate, and fulfils the office of a escapement by maintaining the motion of the pendulum. Thus we see that the principle of this escapement is radically bad. The force during the greater part of its action is disturbing the rate of the clock without maintaining the motion of the pendulum.

If the pallets have such a form that the force is constant and = F, we find by Example 9, that the time of vibration is diminished by

Hence it appears that the vibrations are quicker than they would be without the maintaining force: but that if from a diminution of friction, &c. the arc be increased while the maintaining force remains the same, the vibrations are slower. If while the arc remains the same the maintaining force be increased, the vibrations are quicker.

lf the resistance varied as the square of the velocity, the diminution of the arc from that cause (see Example 3.) would be

: and the increase caused by the force F (found in the same manner) would be

. Hence

, whence

Here then the vibrations are performed quicker in the large arcs than in the small ones.

If the force, instead of being constant from c to a and from a to c, varied directly as the distance, putting, in Example 9,

, the time is diminished by

nearly, when c is small: which is almost independent of a. Here then an alteration in the arc of vibration would scarcely affect the clock's rate: but an alteration in the maintaining power would affect it greatly.

We may thus investigate the possibility of a law of resistance that will make the vibrations isochronous, however the maintaining power may vary. Suppose the force on the pallets constant in

the same vibration: then as it is required that the acceleration produced by the maintaining power shall be invariable, we must have

No resistance expressed in positive powers of the velocity will give a diminution of the arc of this form, and therefore it is impossible to make the vibrations isochronous.

Besides the forces already considered, there is the impact on the pallet which takes place at the beat. As this depends on the weight of the wheels, &c., it is impossible to measure it, but we can discover the nature of the effect which it will produce. It may be represented by a force - G, acting through a very small space h at the distance c. It will therefore diminish the time of vibration by

This evidently diminishes as a is increased, and therefore this force produces the same effect as the others.

We have now sufficient data to enable us to form a judgement of the merits of this escapement. It appears that the maintaining power will always enter into the expression for the time of vibration: consequently, any obstruction or friction of the wheelwork will affect the rate of the clock. The arc also generally enters, and therefore any alteration of the extent of the vibration

will alter the rate. And with the usual form of the pallets no law of resistance can be found which will make the vibrations isochronous.

In Cumming's escapements, the action of the wheels raises a weight through a small space. It is then carried up by the pendulum, and descends with the pendulum, till the latter has arrived at its lowest point. This case, then, is almost exactly the same as the last, with this exception, that the force which acts on the pendulum is independent of the irregularities in the force transmitted through the wheel-work. If, however, the length of the arc of vibration undergo any change, the time of vibration will be changed. The principle of this construction is, therefore, almost as bad as that of the former.

We now come to the dead-beat escapement. Here the wheel acts on the pallet for a small space near the middle of the vibration: and during the remainder of the vibration it has no effect except in producing a slight friction. The impact also at the beat does not tend to accelerate or retard the pendulum. Neglecting then the consideration of the fraction, we have a constant force F, which begins to act when

, and ceases when

. Taking

This is a quantity extremely minute. For c and c' are generally small compared with a, and c' - c may be made almost as small

as we please; consequently

is very small. If c and c' were equal, the effect on the time would be absolutely nothing. With this escapement, therefore, the effect of the maintaining power on the rate of the pendulum may be made as small as we please.

It cannot, however, be made absolutely nothing. For the wheel must be so adapted to the pallets, that when it is disengaged from one it may strike the other, not on the acting surface, but a little above it. That is, the instant of disengagement from a pallet must follow the instant at which the pendulum is in its middle position by a rather longer time than that by which the instant of beginning to act preceded it. Therefore c' must be rather greater than c. But the difference may be made so small that the effect on the clock's rate shall be almost insensible. This escapement therefore, approaches very nearly to absolute perfection: and in this respect theory and practice are in exact agreement.

The impact at the beat indirectly affects the time of vibration by producing, for a very short time, a considerable friction. This cannot be estimated: but it will easily be seen that, as it takes place after the pendulum has passed its lowest point, its effect is to diminish the time of vibration.

As the force of the spiral spring on a watch balance is (in the best springs) proportional to the angular distance of the balance from its position of rest, the same equations which apply to the motion of a pendulum will apply also to the motion of a balance. The comparative merits of watch escapements can, therefore, be determined in the same manner as those of clock escapements. The common crown wheel and verge escapement is precisely similar in its action to the recoil escapement; of clocks, and has exactly the same defects. Mudge's detached escapement for watches is exactly similar in principle to Cumming's

for clocks, with this exception, that the force varies as the distance from the middle position. Putting e x for this force, and observing that it retards the balance from the distance c to a, and then accelerates it from a to 0, we find for the proportionate increase in the time

The first of these terms is large, but invariable: the second, which is variable, is not so small as at first sight it appears. For it will be found that the arc of semi-vibration is increased by

: and this must be equal to A, the quantity by which the arc of semi-vibration is diminished by friction, &c. The product e c ² is, therefore, of the same order as A, and, therefore, the term

is of the order c A, which is not to be neglected. The only variable quantity in this term is a: if from an alteration in the quantity of friction, &c., the length of the arc be increased, the time of vibration will be increased, but c will be a multiplier of the expression for the increase. This, therefore, so far as the theory is concerned, is a pretty good construction. Graham's cylinder escapement, and Mudge's lever escapement (now extensively used under the name of the detached lever), possess almost exactly the same properties as the dead-beat escapement of clocks, and are therefore, very good. The duplex escapement is an instance of a class differing from all those which we have mentioned in one important respect - the maintaining power acts on the balance only once in two vibrations. For the rest, its action (like that

in the dead-beat escapement) lasts for a very short time. It is therefore, in the power of the artist to construct it in such a manner that the action shall take place equally before and after the time at which the balance reaches the middle of its vibration. In this manner the quantities c and c', in the investigation for the dead-beat escapement, would be equal, and the effect of the maintaining power on the rate of the chronometer would be absolutely nothing. It appears to be owing to this that the duplex escapement is found to be so good. The only point in which the detached escapements of Arnold and Earnshaw appear to be superior (which is, however, a point of importance) is the almost perfect absence of friction. As the wheel touches the balance only once in two vibrations the latter may be so adjusted that the time of vibration shall be perfectly independent of the maintaining power. If the slight resistance offered by the springs be taken into account, the same is true. When to this consideration we add that the motion of the balance is not clogged by any friction, except that of its own pivots and spring, it does not appear possible to form an escapement more perfect in theory than these. The reasons which determine tbe form of the teeth of the wheel in these two escapements are entirely practical: provided the action takes place during a small part only of the vibration, it is indifferent whether the force be uniform or not.

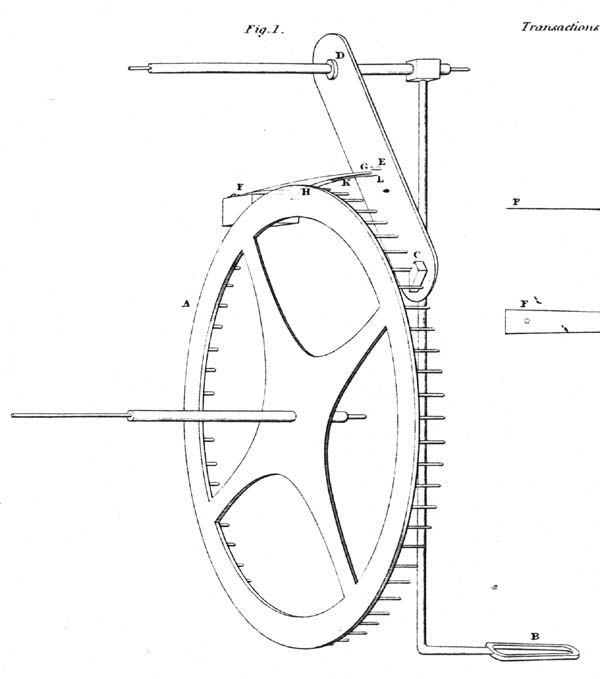
We have seen that the rank which is assigned to the different escapements by theory is precisely the same as that which is given by experience: and this circumstance seems to justify us in the presumption that nothing important is omitted in the view that we have taken of this theory. Perhaps then I may be allowed to suggest, on mere theoretical considerations, a form for the escapement of clocks: similar in its principles to the best detached escapements of chronometers, and apparently likely to possess the same advantages. In fig. 1, A is the wheel whose axis

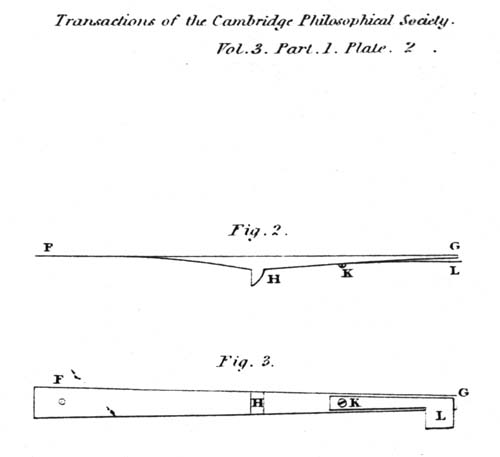
carries the seconds' hand: It is represented in the figure with 60 pins perpendicular to its plane: instead of a wheel with pins, a crown wheel can be used. B is the crutch for the pendulum in its position of rest. C the pallet, carried by the arm CD: in the position of rest it will be between two pins of the wheel. E a small pin carried by the arm CD. FG a spring fixed at F: flexible towards F, and stiff in the remaining part: it carries a tooth H concealed in fig. 1, by the rim of tlte wheel, but shewn in fig. 2: this tooth stops the wheel A by catching one of its pins. KL a very weak spring attached at K to the under side of FG: the part at L projects beyond the rest, that it may be touched by the pin E. The action of this escapement is very simple. When the pendulum moves so that C approaches the center of the wheel, the pin E touches L, and (as the spring KL is very weak) passes it without any sensible retardation. When it returns, immediately before the middle of its vibration, the same pin touches the under side of L, and as L cannot yield without raising FG, it lifts the tooth H from the pin of the wheel which it held, and the wheel thus set at liberty immediately acts on the pallet C Before it has finished its action, the pin F has let go the spring L, and H has descended so as to catch another tooth as soon as the action shall have ceased. The pendulum, it is plain, receives but one impulse in two vibrations, and, therefore, for a seconds' beat, a half second pendulum would be necessary.

To investigate the effect of these actions on the time of vibration, omitting nothing, let z be the distance of the pendulum from its middle point when the action on the pallet begins, z + c that when it ends, z - e the mean distance at which the resistance of the spring FG takes place, and z - k that at which the resistance of KL takes place as the pendulum returns. Let the action on the pallet be supposed constant and = F: and for the springs,

let the product of the force by the space through which they continue their action be G and K respectively. Here c, e, and k depend on the construction of the clock, and z on the situation of the pallet when the pendulum is at the middle of its vibration, that is, on the position of the clock. Observing that when the pendulum is going, we must take

for the proportionate increase, and observing that the first and third forces are positive, and the second negative we find for the proportionate increase

It appears, therefore, that the same of action on the pallet before the pendulum reaches the middle point must exceed, by a very small quantity, that after it has passed the middle point, in order that the time of vibration may be independent of the maintaining force. If the action began before this time, there would be a term of the form

, or

nearly, in the time of vibration: that is, the clock's rate would be made quicker, but less for large

cs than for small (supposing F to be unchanged): to be unchanged): if the action began after it, the contrary effect would take place. If we take for F a force sufficient to counteract the resistance of the air supposed to be as the square of the velocity; since the diminution of the arc from that cause = m a ², the the increase from the action of

, we must have

, or

;

is independent of a and the clock's rate would be the same under all variations of the maintaining power. If the resistance be supposed to follow any other law, the clock's rate will not be independent of a, except the action takes place as is above described.

1st. It would not require greater delicacy of workmanship, perhaps less, than the common dead-beat.

2d. It possesses in theory all the advantages of the detached escapement in watches.

Whether the shortness of the pendulum for a given rate of beat would be any disadvantage, I do not know. The construction would, however, I apprehend, be very convenient for a portable clock. It is evident that by a repetition of this construction, the clock might be made to beat at every vibration: but several advantages would be lost by this complication.

Transactions of the Cambridge Philosophical Socity
Vol. 3, Part 1, Plate 2, Fig. 1.

Transactions of the Cambridge Philosophical Socity
Vol. 3, Part 1, Plate 2, Figs. 2, 3.

The following work is in the public domain.
The reprint of it here, including the TeX encoding for the equations, is dedicated to the Public Domain.
Important disclaimers of warranty and liability in the presentation of public domain material.

Airy, George Biddell. "On the Disturbances of Pendulums and Balances, and on the Theory of Escapements." Transactions of the Cambridge Philosophical Society Vol. III, Part I (1830): 105-128, Plate 2.

lemur.com is a service mark of David M. MacMillan and Rollande Krandall.
Other trademark recognition.

Presented originally by lemur.com.^SM

Airy On Pendulum and Balance Wheel Theory

III1 On the Disturbances of Pendulums and Balances, and on the Theory of Escapements.

III¹ On the Disturbances of Pendulums and Balances,
and on the Theory of Escapements.