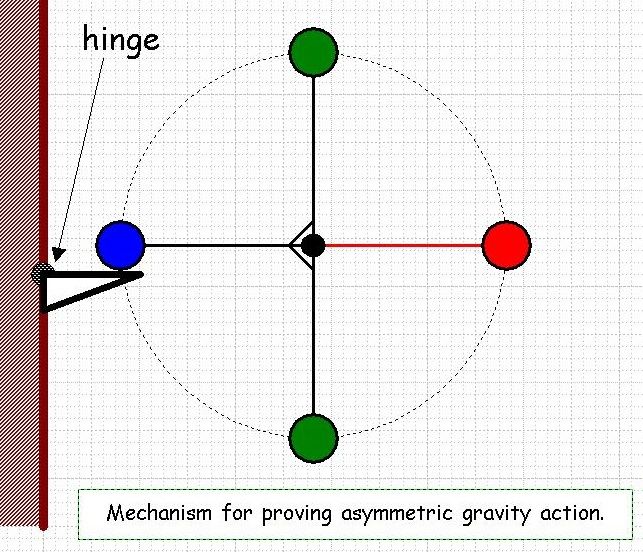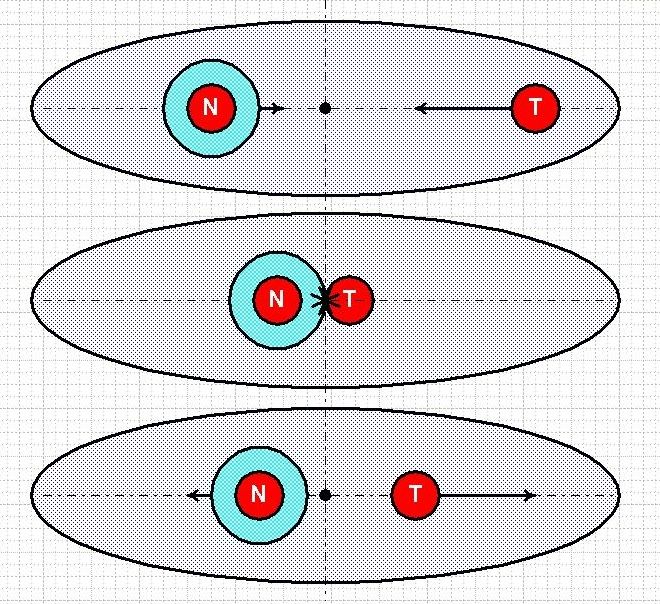
The above diagram shows the three stages of angular momentum (AM) transfer for the non-one way clutch case. In other words the case where both the single 3 o'clock weight (T) and the combination 9 o'clock and balanced weights (N) are free to rotate.
You will notice that the weights are surrounded by a elliptical grey area. This represents the weights taken as a whole, the Group, and must be thought of as a real independent hierarchical entity. Anyone familiar with Analysis of Variance will recognise these two different levels as analogous to the concept of within and between batch variation.
Because this is a closed system for rotation AM has to be conserved.
Therefore the Group Centre (represented by the black dot) has to remain stationary throughout any elastic interaction of the weights. This applies to any elastic interactions whatever, not just the particular interactions being considered here.
Turning now (no pun intended) to the interaction shown in the diagrams above.
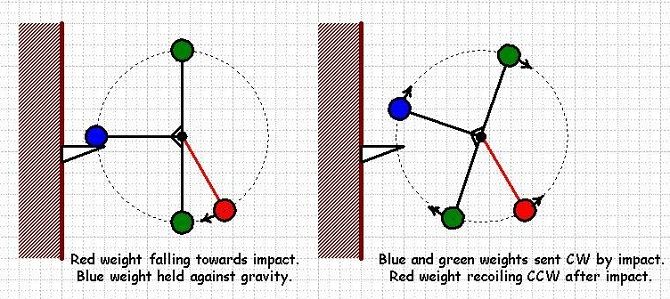
The T weight moves CW to the elastic impact point. At the same instant the N weights move CCW to the impact point.
Say the T weight carries 5 units of CW AM. Because angular momentum must be conserved the N weights must carry 5 units of CCW AM.
If we designate CW AM as positive and CCW AM as negative then the algebraic angular momentum is zero. The Group Centre is stationary.
At elastic impact between T and M the angular momentums are exchanged.
T moves off to the right towards its reset position with N's -5 units of AM and N moves off to the left with T's +5 units of AM.
Now even if T regains its reset position so that once again the wheels are perfectly balanced there will be no net angular momentum for the 6 weight wheel.
To sum up. There can be no angular momentum gain, no rotational energy gain in other words, for a wheel system which is rotationally closed, rotationally isolated.
One has to open up the system.
Moreover, one has to open up the system asymmetrically so that the gravitational wind can do work on one side and be prevented from doing work on the other.
This can be achieved by introducing a one way clutch to the system so that gravity can do work on the T weight and be prevented from doing work on the N weights.
The interactions for such a system are shown in the next set of diagrams.

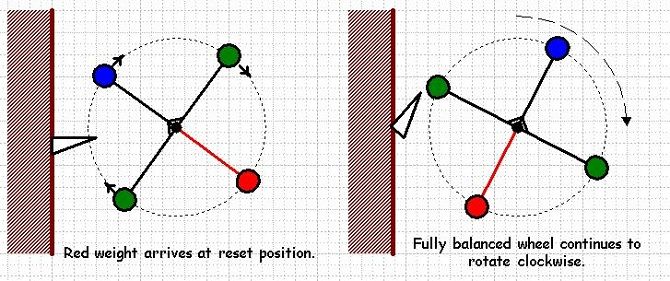
In this case the N combination is stationary as shown. the T weight moves towards impact as before carrying 5 units of CW AM. The N combination is prevented from moving CCW so it provides no AM to the system.
At impact the one way clutch allows the N combination to move CW. Impact switches the weight system from being open to being closed in respect of AM.
The angular momentum of the 6 weight system is not conserved with respect to our external frame of reference though it is of course with respect to the internal grey ellipse frame of reference.
The group centre will now continue to move clockwise with a total AM of 5 units and this will not be attenuated in any way by elastic interactions of N and T.
We know therefore that it must be possible to return T to its reset position. If we do this in such a way as to reduce the velocity of T relative to N to zero then the now balanced wheel will rotate continuously with an AM of 5 units.
By forcing the Newtonian Gravitational Wind to act asymmetrically we have manifested "perpetual motion".
Of course, knowing why something is certainly possible and achieving it experimentally are quite different things. But knowing why it's possible is certainly a big incentive to overcome the experimental problems which I will be going into in further posts.
Did Bessler's wheel work this way?
I doubt it. I think his solution was more sophisticated and involved pendulums in some form or another. Cloud Camper seems to have some constructive thoughts on this.
Did Kennie's wheel work this way?
Probably.