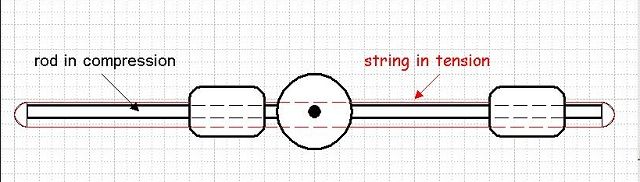
If weights are coupled together as in the above diagram then we have an adiabatic exchange situation. During rotation the energy gain in the weight moving out towards the circumference is equal to the energy loss in the weight moving in towards the centre.
Each weight can move from a short pendulum state to a long pendulum state .
But we have met this adiabatic exchange situation before.
Where?
In the Rubber Band Motor (RBM) - and we know that is a gravity mill, albeit a less than unity one. In other words we put more energy in, in the form of heat to make up for losses, than we are getting out in the form of gravitationally induced rotation. If we perfectly insulate the rubber bands to prevent any heat loss then we will have a perfect adiabatic exchange. We will need to apply some external energy to keep the oscillation horizontal but this can be far less that that generated by the out of balance gravitational forces. In other words we will have achieved overunity.
Clearly the RBM is unlikely to ever be developed into a practical gravity motor. However, not only is the mechanism illustrated in the above diagram a likely candidate, if I understand Bessler correctly, it already has been.
In the case of the RBM the "pendulums" are the atom rotations and the molecule rotations, with energy oscillating between the two. In our case the weights when at the smallest distance from the centre correspond to the atom pendulums and the weights when at the greatest distance from the centre correspond to the molecule pendulums.
Moreover the mechanism is an unstable 2 state flip-flop.
To understand why, think of two equal weights hanging over a pulley in a rotating space station. The weights are being pulled towards the floor by the Ersatz Gravitational Field (EGF). If the diameter of the space station is very large then the EGF gradient will be negligible, just as for example the Newtonian Gravitational Field (NGF) gradient at the surface of the earth is negligible. In both cases the friction at the pulley is sufficient to hold the weights in equilibrium irrespective of the distance between two weights.
On the other hand where the diameter of the space station is only a few yards there is a very intense gradient in the EGF. Its strength decreases rapidly as one moves from the space station floor to the centre. At the very centre the EGF strength is zero. Weights hanging at the same distance from the pulley are in unstable equilibrium. If one of the weights moves down slightly it's subject to a greater Ersatz gravitational force; its partner moving up experiences a lesser force. This difference increases until one of the weight hits the floor or over-tops the pulley
Now if we can flip states at 12 and 6 o'clock then we have the makings of a continuously unstable wheel. To do this we need an additional oscillator in the vertical direction. The RBM provides its own vertical oscillator in the elastic spring of the rubber bands but the above mechanism doesn't have that property so we have to provide it with a spring which balances the NGF. Without such a balancing spring it would immediately keel.
So we have two interacting oscillators, a flip-flop oscillator in the horizontal direction and a conventional spring-mass oscillator in the vertical direction.





