I really like the MT 143 geared levers and wondered what would happen if you mounted a pair of 143 assy’s with two 50 lb levers on top of a heavy 500 lb pendulum. Then install another pair of 143 assy’s near the 500 lb weight for counterbalancing purposes. I have installed a small motor to drive the assy’s at a continuous angular velocity, which is easily variable of course. The motor is not connected to the load except in a secondary fashion, this is similar to the Milkovic device. The motor has no intelligence in the sim as to what the 500 lb pendulum is doing. This is similar to the Milkovic design in that there is only an indirect connection between the secondary (input) and primary (output) system.
The potential OU aspect is that both pairs of 143 geared lever assy’s are all driven together off the same motor thru a pair of common chains (the green lines in the diagram) so wherever the 500 lb pendulum is located, there is no work required to rotate the 143 assy’s. We are getting the overbalancing for free minus friction of course.
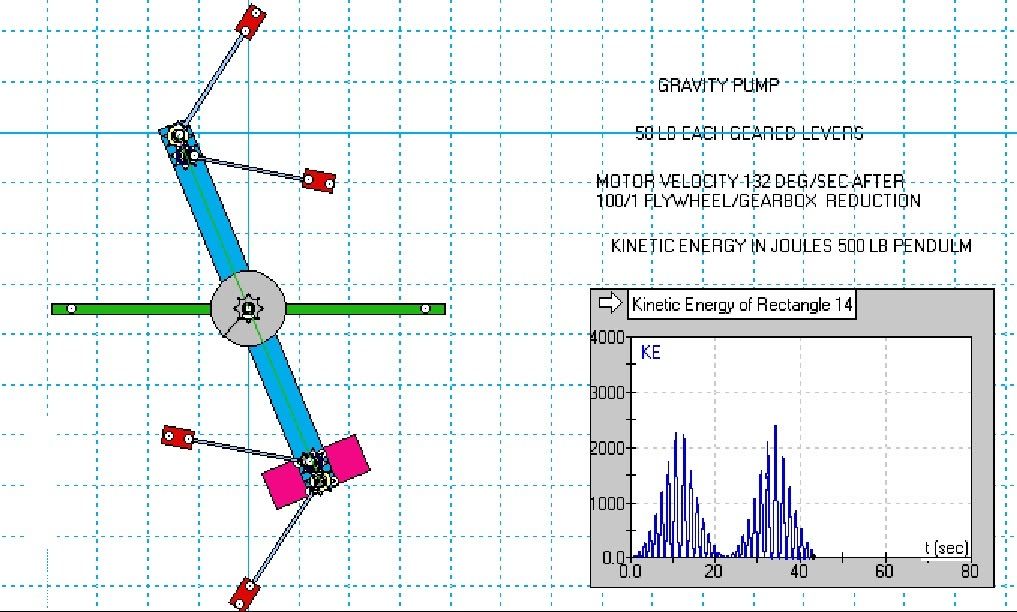
Wherever a 143 assy is ascending, the other is descending. The weighted levers in each 143 assy naturally counterbalance the other lever as long as they stay in a vertical alignment. By adding the second 143 assy we create a counterbalance for the entire secondary system, no matter the orientation or location of the main pendulum. Whatever one weighted lever is doing, there is another doing the exact opposite. What does not counterbalance is the CoG of the system. We are producing massive CoG changes nearly free.
With the Milkovic design, the input pendulum must be excited by hand at just the right time to keep the output in resonance. With this rotary analogue, a simple motor can do it with electronic controls. The motor is run at idle power, just enough to overcome the friction in the system. The motor is not under any load. There would be CF effects at higher speeds but this system is designed to operate at a very low speed, minimizing any CF buildup. The goal is massive torque here, not rpm.
There is an unknown small amount of secondary (acceleration) forces occurring that are moderated by the 200 lb flywheel rotating 100 times faster than the MT143 assy’s located at the fulcrum. So now we have all the primary forces counterbalanced out and hopefully most of the secondary forces. Most of the secondary forces should self cancel anyway as there is an equal amount of deceleration as accel.
In the graph for KE output, I have set the units in Joules because of a WM2D labeling problem with BTU’s. 1 Joule = .000948 BTU for the BTU fans out there. The following animation can be clicked on to start it.

The system is highly sensitive to the rotation speed of the motor. Just a change of 5 degrees per second in motor speed can create a huge effect on the 500 lb pendulum, driving it almost over the top from a dead stop within about 4 1/2 full swings if the right excitation speed is chosen. If a velocity of 125 deg/sec is chosen, a maximum KE of only 700 Joules is attained. Bumping it up to 132, KE jumps to 2264 Joules. This is at the resonance condition for the system.
Then once the system is up to speed, the computer controlled motor will keep the system in the sweet spot. The motor speed needs to slow down slightly once it achieves resonance. With no controls at all as in the sim, the motor then overdrives the pendulum after achieving the resonance condition and then begins actively wasting energy slowing the pendulum down until it has no energy at all!
But if we take note of the full period pendulum swing (2.7 sec) and the amount of KE increase on the last full swing (1063 joules) we get an increase of 394 joule/sec. Then since 1055 joule/sec = 1.414 hp, we can get a theoretical .53 hp continuous output if the system is maintained at resonance. And of course that does not take into account the input energy which should be small or working/air friction. The drive motor is only spinning at 35 rpm under no load other than friction so I’m wild ass guessing 125 watts which is .17 HP. So we have roughly/possibly a 3/1 potential COP. Lots of mass to generate half a horsepower but
that’s the way it is in the gravity power biz.
On an actual device one would limit the massive pendulum’s arc to maybe 270 degrees which would reduce to around 180 with a load applied, as an
arc of greater than 270 degrees wastes too much time in lateral translation. This would be done by installing a permanent magnet AC alternator at the fulcrum, which would generate output in both directions which would be then rectified to DC thru a full wave rectifier. A pair of these units side by side swinging in opposite phase would largely eliminate imbalance in the support structure. Air friction (windage) would be a very minor factor as velocities are low. The motor driving the system is located at the exact fulcrum to prevent it’s weight from reducing efficiency.
The motor driving the geared levers would be controlled for velocity by computer controlled circuitry which would keep the 500 lb pendulum in the sweet spot, or maximum resonance condition depending on load. One can observe from the KE window the sharpness of the resonance peak and that the energy quickly deteriorates when the excitation speed is not perfect. This is a job for electronic controls! A typical motion control system can control up to eight separate motors so a single control system could control 8 gravity pumps in a row. This would also divide up the computer overhead over 8 systems.
Banks of these units could be installed in a small area or even underground to create a gravity farm. It would look similar to rows of oil well pumps churning away but pumping gravity instead of oil! A 4 unit side by side pump weighing 3 tons in a backyard shed might support powering a small home (2 hp – 1500 W). A large solar or wind power setup can weigh that much. And of course, power is continuous, not dependent on erratic wind or solar conditions.
Of course a computer simulation means squat until a physical rep is done. It’s unknown at what level power could be extracted without destroying the resonance condition. However it doesn’t seem to bother the Milkovic oscillator to drive the twelve flashlights. Perhaps a program could be written in the WM2D scripting language to adjust the motor speed in the simulation to keep the system at the maximum resonance condition. That will take a bit of time. A continuous load may then be applied in both directions to simulate the AC alternator.
In a physical rep, the excitation velocity would probably change under load and the computer controlled motor could be setup to follow a lookup chart or spreadsheet that would adjust to different load and speed conditions. Or it could be controlled by simple microswitches or hall effect sensors that would simply bump the speed up or down like a thermostat or just switch the alternator load on and off to maintain the resonance condition. This would be the cheap and dirty way to go.
I have a couple of the older heavy 3 phase wheelchair motors that have very high torque but low rpm so these might be ideal to use as an AC alternator. I wired both motors together the other day thru the 3 phase, then turned one of them with a drill press motor. The second motor turned one for one with the driven motor at a very low rpm and worked bi-directionally so it looks feasible.
Now where did I leave that 500 lb pendulum? I knew I would need it for a cool project someday!

