Priority Claim
Moderator: scott
re: Priority Claim
You guys have at it! I am still stuck on Dunesbury's question: How do you keep a stator stationary while the rotor turns making for EMF?
Lenz law says; impossible, you would still need a power source.
Lenz law says; impossible, you would still need a power source.
- cloud camper
- Devotee

- Posts: 1083
- Joined: Tue Mar 15, 2011 12:20 am
Re: re: Priority Claim
No Bill, you are confused between angular momentum and rpm of the wheel.ovyyus wrote:Really? Lifting a weight against CF (earthbound eg: spinning ice skater pulls arms inwards) would cause the space station to increase angular momentum. The increase is proportional to the work done. Therefore, no energy is "lost".CC wrote:Now we stop the rotation of the space station. We never added any angular momentum to the station but now all the internal GPE we added thru biological work is "lost".
Retracting the skaters arms overhead reduces radius of gyration, bringing the center of mass closer to the CoR. This increases rpm of the wheel.
But since angular momentum is a conserved quantity, there is no energy added. When radius of gyration is decreased, the wheel rpm
increases to preserve overall angular momentum. When the radius is increased, the wheel slows down, still preserving AM (designated L in physics books).
This is because doing work against CF is at 90 degree angle to the angular momentum vector. When vectors are at 90 degrees to each other, changing one vector creates no effect on the other.
Doing work against CF within a rotating wheel creates GPE within the wheel but this GPE does not translate to increased AM since the vectors are at 90 degrees to each other.
Last edited by cloud camper on Fri Aug 08, 2014 11:42 pm, edited 1 time in total.
re: Priority Claim
You're right CC, my bad. I should have said RPM, not angular momentum.
- cloud camper
- Devotee

- Posts: 1083
- Joined: Tue Mar 15, 2011 12:20 am
re: Priority Claim
No worries Bill.
I'm just glad we finally agree on something!
I'm just glad we finally agree on something!
Re: re: Priority Claim
Full marks to Bill for realising he'd got it wrong - and to cc for explaining why.ovyyus wrote:You're right CC, my bad. I should have said RPM, not angular momentum.
An example to all of us.
Who is she that cometh forth as the morning rising, fair as the moon, bright as the sun, terribilis ut castrorum acies ordinata?
Re: re: Priority Claim
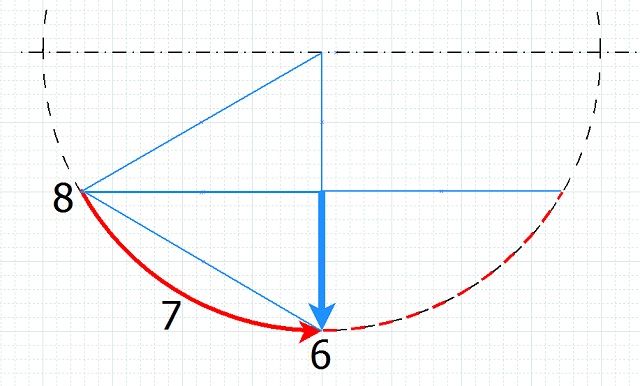
One interesting thing about those images and the video from which they came is that the curvatures are relatively small. Had he increased the curvature he would have shown that the transit time passed through a minimum at the brachistochrone (cycloid). Both the red paths in the figure below are slower than the blue.Grimer wrote:Pendulums don't have to be constrained to swing about their centre of curvature by a string in tension. They can alternatively swing about their centre curvature constrained by a slope in compression.
Realising this, and the implications, is the key to understanding the High Road - Low Road videos.
The above image shows 1 second, 2 second and 3 second stringless pendulums.

Who is she that cometh forth as the morning rising, fair as the moon, bright as the sun, terribilis ut castrorum acies ordinata?
re: Priority Claim
Even though there is a difference in time, there is still no difference in comparative KE vs initial PE. Without energy gain, there is no extra movement. What advantage do you see here?
re: Priority Claim
I see that Fletch is on a charge. I'd better pull my finger out before I'm overtaken, eh! :-)
Fortunately I now see how to use the simple pendulum's pull rather that its push. In other words I'll be moving from the Keenie to the Bessler solution.
Who is she that cometh forth as the morning rising, fair as the moon, bright as the sun, terribilis ut castrorum acies ordinata?
re: Priority Claim

This image is pretty well self explanatory for members familiar with the Milkovic pendulum and the GPM - Mark 2.
A ground based ratchet (not shown) catches the simple pendulum on the apogee of its counter-clockwise back swing so that it can be picked up by the compound pendulum as it rotates clockwise and perfectly balance the pendulum.
The swing of the simple pendulum has been set at 60° from apogee to nadir. This is approximately the same as the swing of a cycloid pendulum and ensures that there is the maximum time difference between the compound and simple pendulums.
There is a trade off between the speed of the swing and the strength of the Ersatz gravity pulse produced. For example, a 180° swing would give a pulse of double the strength of the 120° swing shown. Experimentation will find the optimum value for these two variables.
It is interesting that the Milkovic pendulum is generally shown as having a 120° swing. Perhaps the inventor subconsciously felt for the optimum point - a bit like the instinctive way people learn to balance on a bicycle.
I seem to remember writing something about this.
Here it is:
That's quite useful. It confirms the value of the downward pull. One unit of Newtonian Gravity and one unit of Ersatz Gravity.Grimer wrote:I don't really want to add two pounds but only one. I want to reduce the swing so that a one pound counterweight will oscillate with two pounds at the nadir and zero pounds at the zenith.Grimer wrote:Its a long time since I took sixth form dynamics so I have to take these things slowly.
Based on Jonathan's post here:
http://www.besslerwheel.com/forum/viewt ... =8009#8009
Jim is right, it is true. If, instead of resorting to calculus, we assume that gravity is a conservative field, then we have
.5m(v^2)=2mgR --> (v^2)=4gR
Fc=m(v^2)/R=4mg
for a pendulum falling from 12 to 6. If mg=1lb, then Fc=4lbs at the nadir.
Now I'm interested in a mass falling from 3 or 9 to 6 so I'll rewrite the above
for my case. I'll try to write them as close as possible to the way I would have
written them at school.
½.mv² = R.mg
Cancelling m on both sides and bringing over the half
v² = 2gR
Acceleration = v²/R = 2gR/R = 2g
therfore Ersatz Gravity (EG)
EG = mass x acceleration = 2mg
So of a mass of 1 lb EG adds 2 lb.
Quite a lot really.
The anti-intuitive aspect is that the amplification of force is independent of the radius.
As the diagram below shows to achieve this I have to reduce the 9 to 3 swing to a 8 to 4 swing. This reduces the swing drop angle from 90° to 60°. Interestingly this is about the angle that Milkovic and Raymond seem to adopt. Maybe they instinctively feel for the optimum.

As you can see from the above diagram the traditional Milkovic pendulum does not have the necessary extension to allow it to be caught at the balanced beam point, the point where unused energy in the compound pendulum would allow 360° rotation to the reset point.
A simplified version of the extended Milko is given below.

It's the inverse of the phenomenon we get with the Gravity Pulse Motor, inverse in the sense that the GPM uses push whereas the Milkovic uses pull.
Perhaps the following post from the General Discussion Forum will make things clearer
*******************************************************Grimer wrote: It's not a two stage oscillator, it's a three stage oscillator:
Simple Pendulum, A
Compound Pendulum, B
and Balanced Beam. (A+B) = C
A three stage teapot.
Lid (simple pendulum)
Body (compound pendulum)
Teapot (balanced beam)
The balanced beam is the boundary case of a compound pendulum.
Asymmetric warfare
The essential strategy of the GPM and its inverse the extended Milkovic and the Bessler can be viewed as an example of asymmetric warfare. A small section of the whole (the simple pendulum) breaks away from the whole to attack the remaining body (the compound pendulum) by push in the case of the GPM, by pull in the case of an extended Milko and the Bessler. The small section then melts back into the whole before the body can get round to attacking it back.
And now I'd better get round to preparing a diagram to show how a swinging pendulum can put pulses of energy into a Bessler type wheel.
Who is she that cometh forth as the morning rising, fair as the moon, bright as the sun, terribilis ut castrorum acies ordinata?
re: Priority Claim
Grimer,
I believe a 2SO can be a valid prime mover to either pulse a drum into motion or raise weights in an OB wheel. That said, I believe there are things you will only learn by hands on building and testing. Things you would never foresee in a graphical/mathematical model. For one thing, the pendulum bob will never rise to the same height (relative to the pivot point of the pendulum) from which it was dropped, and this has nothing to do with air resistance or friction.
Attached is one of my early test models. It was cheap to build and it hung on the garage wall. No bearings, just long bolts with smooth shanks. I pre-drilled holes in the main crossbar and pendulum shaft so I could quickly make weight and positions adjustments.
I believe a 2SO can be a valid prime mover to either pulse a drum into motion or raise weights in an OB wheel. That said, I believe there are things you will only learn by hands on building and testing. Things you would never foresee in a graphical/mathematical model. For one thing, the pendulum bob will never rise to the same height (relative to the pivot point of the pendulum) from which it was dropped, and this has nothing to do with air resistance or friction.
Attached is one of my early test models. It was cheap to build and it hung on the garage wall. No bearings, just long bolts with smooth shanks. I pre-drilled holes in the main crossbar and pendulum shaft so I could quickly make weight and positions adjustments.
re: Priority Claim
Here are the WM2D files for Grimers GPM, or at least a prev. version of it.
I disagree with Frank's all knowing sim guy. There is no friction in this sim, and the impact is perfect, as I have said once ot twice before.
I disagree with Frank's all knowing sim guy. There is no friction in this sim, and the impact is perfect, as I have said once ot twice before.
re: Priority Claim
Frank, it is about timing. If the two pendulums met exactly, there would be exactly no energy for rotation. you could also get the same rotational energy by dropping the 1 weight, then catching it in the same position.
re: Priority Claim
OK Frank ..
I looked at Tarsiers sims etc - they appear to be operating as they should.
I checked that there was NO frictions & that Elasticity of collisions was set to maximum, that being 1.00 [steel is 0.95] - so this would duplicate a perfect spring with no losses.
To double check I rebuilt the structures myself in my sim program.
See the pics progression I have posted & run the sim to see what happens - you can change any inputs on screen in the Input boxes.
The Driver/Pendulum swings down losing PE & gaining KE - it impacts the Spar - the collision is perfectly elastic [like a perfect spring between them] - the Spar moves CW slowly - the pendulum rebounds upwards.
The pendulum bob almost reaches the yellow cwt mass [but not quite] - the pendulum falls again & impacts the Spar which is moving CCW slowly by then - this gives the pendulum another nudge [due inertia or momentum transfer] - the Spar rotates CW again very slowly - the pendulum bob rotates CCW [rebounds] until it very nearly meets the yellow cwt mass.
Note the System Kinetic Energy totals in the pics & particularly the sim.
.........................
If you increase the elasticity factor of collisions to above 1.00, say 1.1. or 1.2 you will see a huge energy gain - this is not as silly as it sounds because an old friend of mine [Reiner] many years ago showed me experiments of steel balls dropped onto 'cooled' steel plates - they rebounded higher than their start height i.e. gained PE.
Also there is some site somewhere discussed on this board of spinning weights rising higher than non rotating ones - the guy goes into quite some math & explanation IIRC - perhaps you could look into these phenomena to give your GPM a boost.
Sorry I can't be more upbeat about the principle Frank.
I looked at Tarsiers sims etc - they appear to be operating as they should.
I checked that there was NO frictions & that Elasticity of collisions was set to maximum, that being 1.00 [steel is 0.95] - so this would duplicate a perfect spring with no losses.
To double check I rebuilt the structures myself in my sim program.
See the pics progression I have posted & run the sim to see what happens - you can change any inputs on screen in the Input boxes.
The Driver/Pendulum swings down losing PE & gaining KE - it impacts the Spar - the collision is perfectly elastic [like a perfect spring between them] - the Spar moves CW slowly - the pendulum rebounds upwards.
The pendulum bob almost reaches the yellow cwt mass [but not quite] - the pendulum falls again & impacts the Spar which is moving CCW slowly by then - this gives the pendulum another nudge [due inertia or momentum transfer] - the Spar rotates CW again very slowly - the pendulum bob rotates CCW [rebounds] until it very nearly meets the yellow cwt mass.
Note the System Kinetic Energy totals in the pics & particularly the sim.
.........................
If you increase the elasticity factor of collisions to above 1.00, say 1.1. or 1.2 you will see a huge energy gain - this is not as silly as it sounds because an old friend of mine [Reiner] many years ago showed me experiments of steel balls dropped onto 'cooled' steel plates - they rebounded higher than their start height i.e. gained PE.
Also there is some site somewhere discussed on this board of spinning weights rising higher than non rotating ones - the guy goes into quite some math & explanation IIRC - perhaps you could look into these phenomena to give your GPM a boost.
Sorry I can't be more upbeat about the principle Frank.
- Attachments
-
- gpm2A.wm2d
- Grimer's Gravity Pulse Motor POC
- (21.57 KiB) Downloaded 90 times