Mechanising the maths
Moderator: scott
-
MrVibrating
- Addict

- Posts: 2879
- Joined: Sat Jul 31, 2010 12:19 am
- Location: W3
Mechanising the maths
Earlier today i hit on a simple resolution of the problems i'd previously been working on here. To recap:
• kiiking under CF force, as opposed to gravity, conserves net system angular momentum; all gain in the swing's angular momentum comes at the expense of the angular momentum producing the CF force in question, thus preserving net system momentum.
Which is only to restate the 1st law; that the net angular momentum of a closed system of masses interacting about a common axis is constant WRT time.
When kiiking under gravity of course the angular momentum is gained from gravity's constant acceleration, and time; as such it does represent a real change in net system momentum. However the energy cost of this momentum squares with rising system angular velocity, because CF force squares with RPM, and this maintains perfect energy-symmetry between CF-PE, rotational KE and GPE. That is to say, kiiking under gravity, all else being equal, is inherently energy-conservative. We can gain momentum this way, but for a zero-sum.
Mechanical over-unity however arises only when we can fix the unit-energy cost of angular momentum to an RPM-invariant value; under such a regime, a given onboard input workload will cause a consistent rise in net system momentum per cycle, for the same work-done / input energy cost. For instance imagine a self-propelled cart driven by pedals or, say, pulling a lever - each time you pull the lever you perform the same amount of input work in terms of force times displacement, and each pull causes the same amount of acceleration of the cart. You can even try putting simple numbers on it if you wanted to work through an example: suppose the cart weighs 1,000 kg all-in, that each pull of the lever costs 500 J and accelerates the cart by 1 m/s; pull the lever ten times in a row and you've burned 5 kJ, yet you now have 1 metric ton moving at 10 m/s, hence 50 kJ of KE.. a 10:1 energy gain.
The prospect of such a lever, that always requires the same amount of input work but which causes the same amount of net system acceleration each pull, doesn't seem such a transgression in and of itself, yet because of the quadratic relationship between KE and velocity this seemingly-simple mechanical concession effectively creates and destroys energy ex nihilo.
Yet working backwards from the certain knowledge (or even just the theoretical presumption) that Bessler's art was genuine, there's simply no escaping the fact that some variation on this kind of exploit had to have been in effect; the machines gained momentum, and there was patently less work involved in doing so than their resulting RKE rise.
The fundamental constraint that i hit in trying to embody these principles was that the window of opportunity for purchasing angular momentum from gravity and time inevitably shrinks inversely to RPM; the faster the system turns, the less time the OB moment spends under gravity's constant acceleration each cycle, hence the same amount of input work in terms of raising mass against gravity, achieves diminishing angular momentum returns the more of the stuff we accumulate.. Capiche?
In other words the 'trick' implicitly involves isolating the internal members gaining the momentum from gravity and time, from the OB system and the wheel's own angular velocity.. The things inside the wheel that are gaining energy - the over-unity components - must be moving at a velocity that is independent of the net system RPM and the tumbling gravity vector in relation to the system's rotation.
And so if you've followed all that you're now in a position to grasp why i'm optimistic about the connection i may have made earlier:
• CF kiiking may not alter net system angular momentum, but over-balancing obviously does; what happens when we mix them?
Consider a wheel containing a pair of pendulums, counter-balanced against one another's gravitation such that they only 'feel' the artificial-gravity of CF force.
Rather than simply setting them swinging, we're going to kiike with them, by giving them independently-variable moments of inertia; changes in MoI whilst rotating incur the ice-skater effect, causing upswing vs downswing period differences and thus gaining or shedding momentum - a la 'pumping the swing' - over each full swing cycle. As noted, gains in CF swing momentum come at expense of wheel angular momentum, but if we also have an OB system onboard then that momentum's obviously being replenished.. and thus the momentum being gained on the swings is effectively still being sourced from gravity and time, just via the intermediary of CF force!
Kiiking under CF is not a lost cause if you also have an OB system to constantly add more momentum!
This in turn means that the oscillating speed of the pendulums can be independent of or asynchronous to the wheel's RPM and the GPE / OB cycle.
Suppose these pendulums in turn drive a simple crank-operated OB system, converting consistent angular motion into an OB action as i was investigating in my last thread here.. some form of one-way bearing or ratcheting mechanism could be employed to rectify only the 'power strokes' when the pendulum MoI's are retracting..
To make an analogy it'd be like riding the park swing, gaining a little height with each full cycle, but instead of accumulating the gains, suppose you give a kick to a hefty flywheel alongside you, applying your momentum gains to it rather than keeping them yourself.. hence your swinging speed never actually increases, this other rotating body is being accelerated instead..
Here, instead of exchanging the momenta via collisions we're raising weights in an OB system, so converting swing momentum gains into GPE gains and then back into rotKE gains.
In terms of energy dynamics, the types of simplified OB systems i've previously demonstrated here may be considered equivalent to a simple rotating action; it's basically a crank-driven piston system wherein the 'pistons' are OB weights moving in and out, and the 'crank' is a flywheel that's actually embodying the angular momentum being farmed at discount energy cost; it is thus not the wheel body itself that is over-unity, but this internal flywheel-plus-OB weights system; specifically the angular component of that flywheel's motion. The GPE game of course remains a zero-sum.
This, it seems, may be a good fit for the 'differently-applied children's game'.. (the upturned whistling top on the Toys page)
The flail that wants to be with the thresher not the scholar is the vMoI action, and its resulting reactionless torque which needs rectifying in a consistent angular direction on the internal flywheel flinging the OB weights in and out.
The 'square' glyph replete throughout MT pertains to oscillating actions, these consisting of four discrete inertial interactions - two accelerations and two decelerations - each full cycle. Each of these inertial interactions is an opportunity to ply force*time asymmetries..
..and the children with heavy clubs are CF kiikers, driving the internal flywheel-plus-OB weights system via a one-way slip mechanism like a ratchet.
In a nutshell, the intended exploit is to fix the unit-energy cost of the angular momentum being accumulated on that internal flywheel-plus-OB system to a value independent of the wheel's RPM, so the CF pendulums will swing at some preferential speed, oscillating back and forth, and the wheel RPM will be accelerated up to speed only by the action of OB torque. It's the internal flywheel and the linear action of the weights it's cranking in and out that is intended to break unity, since the work being performed against CF force is decoupled from the wheel RPM and its diminishing G-time per cycle with rising RPM. If it works, the sum of the net work performed against CF force will be less than the rotKE gained from over-balancing..
I'll start knocking up a sim when i get the chance, W/E maybe..
• kiiking under CF force, as opposed to gravity, conserves net system angular momentum; all gain in the swing's angular momentum comes at the expense of the angular momentum producing the CF force in question, thus preserving net system momentum.
Which is only to restate the 1st law; that the net angular momentum of a closed system of masses interacting about a common axis is constant WRT time.
When kiiking under gravity of course the angular momentum is gained from gravity's constant acceleration, and time; as such it does represent a real change in net system momentum. However the energy cost of this momentum squares with rising system angular velocity, because CF force squares with RPM, and this maintains perfect energy-symmetry between CF-PE, rotational KE and GPE. That is to say, kiiking under gravity, all else being equal, is inherently energy-conservative. We can gain momentum this way, but for a zero-sum.
Mechanical over-unity however arises only when we can fix the unit-energy cost of angular momentum to an RPM-invariant value; under such a regime, a given onboard input workload will cause a consistent rise in net system momentum per cycle, for the same work-done / input energy cost. For instance imagine a self-propelled cart driven by pedals or, say, pulling a lever - each time you pull the lever you perform the same amount of input work in terms of force times displacement, and each pull causes the same amount of acceleration of the cart. You can even try putting simple numbers on it if you wanted to work through an example: suppose the cart weighs 1,000 kg all-in, that each pull of the lever costs 500 J and accelerates the cart by 1 m/s; pull the lever ten times in a row and you've burned 5 kJ, yet you now have 1 metric ton moving at 10 m/s, hence 50 kJ of KE.. a 10:1 energy gain.
The prospect of such a lever, that always requires the same amount of input work but which causes the same amount of net system acceleration each pull, doesn't seem such a transgression in and of itself, yet because of the quadratic relationship between KE and velocity this seemingly-simple mechanical concession effectively creates and destroys energy ex nihilo.
Yet working backwards from the certain knowledge (or even just the theoretical presumption) that Bessler's art was genuine, there's simply no escaping the fact that some variation on this kind of exploit had to have been in effect; the machines gained momentum, and there was patently less work involved in doing so than their resulting RKE rise.
The fundamental constraint that i hit in trying to embody these principles was that the window of opportunity for purchasing angular momentum from gravity and time inevitably shrinks inversely to RPM; the faster the system turns, the less time the OB moment spends under gravity's constant acceleration each cycle, hence the same amount of input work in terms of raising mass against gravity, achieves diminishing angular momentum returns the more of the stuff we accumulate.. Capiche?
In other words the 'trick' implicitly involves isolating the internal members gaining the momentum from gravity and time, from the OB system and the wheel's own angular velocity.. The things inside the wheel that are gaining energy - the over-unity components - must be moving at a velocity that is independent of the net system RPM and the tumbling gravity vector in relation to the system's rotation.
And so if you've followed all that you're now in a position to grasp why i'm optimistic about the connection i may have made earlier:
• CF kiiking may not alter net system angular momentum, but over-balancing obviously does; what happens when we mix them?
Consider a wheel containing a pair of pendulums, counter-balanced against one another's gravitation such that they only 'feel' the artificial-gravity of CF force.
Rather than simply setting them swinging, we're going to kiike with them, by giving them independently-variable moments of inertia; changes in MoI whilst rotating incur the ice-skater effect, causing upswing vs downswing period differences and thus gaining or shedding momentum - a la 'pumping the swing' - over each full swing cycle. As noted, gains in CF swing momentum come at expense of wheel angular momentum, but if we also have an OB system onboard then that momentum's obviously being replenished.. and thus the momentum being gained on the swings is effectively still being sourced from gravity and time, just via the intermediary of CF force!
Kiiking under CF is not a lost cause if you also have an OB system to constantly add more momentum!
This in turn means that the oscillating speed of the pendulums can be independent of or asynchronous to the wheel's RPM and the GPE / OB cycle.
Suppose these pendulums in turn drive a simple crank-operated OB system, converting consistent angular motion into an OB action as i was investigating in my last thread here.. some form of one-way bearing or ratcheting mechanism could be employed to rectify only the 'power strokes' when the pendulum MoI's are retracting..
To make an analogy it'd be like riding the park swing, gaining a little height with each full cycle, but instead of accumulating the gains, suppose you give a kick to a hefty flywheel alongside you, applying your momentum gains to it rather than keeping them yourself.. hence your swinging speed never actually increases, this other rotating body is being accelerated instead..
Here, instead of exchanging the momenta via collisions we're raising weights in an OB system, so converting swing momentum gains into GPE gains and then back into rotKE gains.
In terms of energy dynamics, the types of simplified OB systems i've previously demonstrated here may be considered equivalent to a simple rotating action; it's basically a crank-driven piston system wherein the 'pistons' are OB weights moving in and out, and the 'crank' is a flywheel that's actually embodying the angular momentum being farmed at discount energy cost; it is thus not the wheel body itself that is over-unity, but this internal flywheel-plus-OB weights system; specifically the angular component of that flywheel's motion. The GPE game of course remains a zero-sum.
This, it seems, may be a good fit for the 'differently-applied children's game'.. (the upturned whistling top on the Toys page)
The flail that wants to be with the thresher not the scholar is the vMoI action, and its resulting reactionless torque which needs rectifying in a consistent angular direction on the internal flywheel flinging the OB weights in and out.
The 'square' glyph replete throughout MT pertains to oscillating actions, these consisting of four discrete inertial interactions - two accelerations and two decelerations - each full cycle. Each of these inertial interactions is an opportunity to ply force*time asymmetries..
..and the children with heavy clubs are CF kiikers, driving the internal flywheel-plus-OB weights system via a one-way slip mechanism like a ratchet.
In a nutshell, the intended exploit is to fix the unit-energy cost of the angular momentum being accumulated on that internal flywheel-plus-OB system to a value independent of the wheel's RPM, so the CF pendulums will swing at some preferential speed, oscillating back and forth, and the wheel RPM will be accelerated up to speed only by the action of OB torque. It's the internal flywheel and the linear action of the weights it's cranking in and out that is intended to break unity, since the work being performed against CF force is decoupled from the wheel RPM and its diminishing G-time per cycle with rising RPM. If it works, the sum of the net work performed against CF force will be less than the rotKE gained from over-balancing..
I'll start knocking up a sim when i get the chance, W/E maybe..
Re: Mechanising the maths
.
.
.
The prospect of such a lever, that always requires the same amount of input work but which causes the same amount of net system acceleration each pull, doesn't seem such a transgression in and of itself, yet because of the quadratic relationship between KE and velocity this seemingly-simple mechanical concession effectively creates and destroys energy ex nihilo.
Last edited by WaltzCee on Fri Nov 03, 2023 8:09 am, edited 2 times in total.
........................¯\_(ツ)_/¯
¯\_(ツ)_/¯ the future is here ¯\_(ツ)_/¯
Advocate of God Almighty, maker of heaven and earth and redeemer of my soul.
Walter Clarkson
© 2023 Walter W. Clarkson, LLC
All rights reserved. Do not even quote me w/o my expressed written consent.
¯\_(ツ)_/¯ the future is here ¯\_(ツ)_/¯
Advocate of God Almighty, maker of heaven and earth and redeemer of my soul.
Walter Clarkson
© 2023 Walter W. Clarkson, LLC
All rights reserved. Do not even quote me w/o my expressed written consent.
-
MrVibrating
- Addict

- Posts: 2879
- Joined: Sat Jul 31, 2010 12:19 am
- Location: W3
Re: Mechanising the maths
The modern pump-action type is using the pump shaft as the stator, hence the angular velocity and input reference frame remains relative to earth - you have to keep increasing the pumping speed to continue accelerating. The old rip-cord type depicted on the Toys page, likewise.
Instead, i envisage a system in which we have pendulums kiiking against CF force - swinging at a consistent rate while scooping up angular momentum via MoI variations, and then dumping these momentum gains not directly into the wheel body's momentum, but into GPE via raising OB weight. The main idea is that CF force can be employed as a kind of reservoir or capacitor - in proxy - for the otherwise-tumbling gravity vector. This may allow kiiking at a regular speed whilst wheel RPM's increase asynchronously. In other words, keeping our input-energy workload to a lower speed than the wheel may peg the input-energy cost of momentum to an RPM-invariant value. Net input energy would then be the sum of the per-cycle CF-PE times the number of cycles, which in turn may be less the rotational KE of the net system.
Gimme a few days to consider the right approach; for instance it occurred to me later last night that a mass bouncing in and out against CF force on a linear bearing can still be coupled to an MoI variation and so swinging isn't necessarily the only way to go..
Instead, i envisage a system in which we have pendulums kiiking against CF force - swinging at a consistent rate while scooping up angular momentum via MoI variations, and then dumping these momentum gains not directly into the wheel body's momentum, but into GPE via raising OB weight. The main idea is that CF force can be employed as a kind of reservoir or capacitor - in proxy - for the otherwise-tumbling gravity vector. This may allow kiiking at a regular speed whilst wheel RPM's increase asynchronously. In other words, keeping our input-energy workload to a lower speed than the wheel may peg the input-energy cost of momentum to an RPM-invariant value. Net input energy would then be the sum of the per-cycle CF-PE times the number of cycles, which in turn may be less the rotational KE of the net system.
Gimme a few days to consider the right approach; for instance it occurred to me later last night that a mass bouncing in and out against CF force on a linear bearing can still be coupled to an MoI variation and so swinging isn't necessarily the only way to go..
-
MrVibrating
- Addict

- Posts: 2879
- Joined: Sat Jul 31, 2010 12:19 am
- Location: W3
Re: Mechanising the maths
..main thrust is simply this: all else being equal, CF force is fictitious, and not a momentum source / sink, unlike gravity, which is a time-rate-of-exchange of momentum, or dp/dt. However couple a continuously OB system to the CF workload, and it effectively becomes a conduit for that real force.. the CF vector effectively becomes a dp/dt, a proxy for the gravity vector, yet which remains relative to the wheel rather than relative to the Earth.. So in principle, you can scoop real angular momentum from CF force when backed up by an OB system, and because it's real it's conserved, even if the armatures scooping it up are rotating at slower speeds than the wheel itself. Instead of dumping it into the wheel body however i envisage dumping it into the effort of raising weights on the OB system.
Precisely how best to implement it needs working through, but that's the general description of the intended exploit. CF force can be tapped as a dp/dt if continuously replenished by an OB system, and this in turn may make it possible to fix the unit-energy cost of angular momentum to an RPM-invariant value..
Precisely how best to implement it needs working through, but that's the general description of the intended exploit. CF force can be tapped as a dp/dt if continuously replenished by an OB system, and this in turn may make it possible to fix the unit-energy cost of angular momentum to an RPM-invariant value..
Re: Mechanising the maths
Ive read many of your previous posts and so your absence was noted and glad to see you back.
Re: Mechanising the maths
dp/dt ?
Re: Mechanising the maths
.
.
ratio of change of momentum to a change in time.
ETA
.
ratio of change of momentum to a change in time.
ETA
MrVibrating wrote:unlike gravity, which is a time-rate-of-exchange of momentum, or dp/dt.
Last edited by WaltzCee on Fri Nov 03, 2023 2:52 pm, edited 1 time in total.
........................¯\_(ツ)_/¯
¯\_(ツ)_/¯ the future is here ¯\_(ツ)_/¯
Advocate of God Almighty, maker of heaven and earth and redeemer of my soul.
Walter Clarkson
© 2023 Walter W. Clarkson, LLC
All rights reserved. Do not even quote me w/o my expressed written consent.
¯\_(ツ)_/¯ the future is here ¯\_(ツ)_/¯
Advocate of God Almighty, maker of heaven and earth and redeemer of my soul.
Walter Clarkson
© 2023 Walter W. Clarkson, LLC
All rights reserved. Do not even quote me w/o my expressed written consent.
Re: Mechanising the maths
.
.
Sep 14, 2023 8:09 pm
https://besslerwheel.com/forum/viewtopi ... bb#p201872
.
Sep 14, 2023 8:09 pm
https://besslerwheel.com/forum/viewtopi ... bb#p201872
waltzcee wrote:I think the crux of it is time. A fast powerful force might spin a long time as a little tortuga passes by to notice it while on the way to see new, different things.
- PM is a function of ∆t
Last edited by WaltzCee on Fri Nov 03, 2023 2:33 pm, edited 2 times in total.
........................¯\_(ツ)_/¯
¯\_(ツ)_/¯ the future is here ¯\_(ツ)_/¯
Advocate of God Almighty, maker of heaven and earth and redeemer of my soul.
Walter Clarkson
© 2023 Walter W. Clarkson, LLC
All rights reserved. Do not even quote me w/o my expressed written consent.
¯\_(ツ)_/¯ the future is here ¯\_(ツ)_/¯
Advocate of God Almighty, maker of heaven and earth and redeemer of my soul.
Walter Clarkson
© 2023 Walter W. Clarkson, LLC
All rights reserved. Do not even quote me w/o my expressed written consent.
Re: Mechanising the maths
.
.
MrVibrating,
Does Mechanising the maths sound similar to an analogue computer designed to throw Wagner's math out the window?
.
MrVibrating,
Does Mechanising the maths sound similar to an analogue computer designed to throw Wagner's math out the window?
........................¯\_(ツ)_/¯
¯\_(ツ)_/¯ the future is here ¯\_(ツ)_/¯
Advocate of God Almighty, maker of heaven and earth and redeemer of my soul.
Walter Clarkson
© 2023 Walter W. Clarkson, LLC
All rights reserved. Do not even quote me w/o my expressed written consent.
¯\_(ツ)_/¯ the future is here ¯\_(ツ)_/¯
Advocate of God Almighty, maker of heaven and earth and redeemer of my soul.
Walter Clarkson
© 2023 Walter W. Clarkson, LLC
All rights reserved. Do not even quote me w/o my expressed written consent.
-
MrVibrating
- Addict

- Posts: 2879
- Joined: Sat Jul 31, 2010 12:19 am
- Location: W3
Re: Mechanising the maths
@Jubat - Hi and thank you..
@Trev - delta p over delta t, or change in momentum over change in time, like WaltzCee said - arguably the distinction between real and fictitious forces. Normally the ice-skater effect obviously trades inertia for velocity, for no net change in momentum. However it may be possible to fix that, via the principles i'm considering here; a reactionless rise in momentum being the singular action transitioning a system from unity minus losses to OU.
@WaltzCee - the maths of conservation obvs aren't 'wrong', but dependent on symmetries, esp. N3 / N1 concerning the conservation of momentum, and in turn, conservation of energy between velocity frames. Because energy squares with velocity, the sum of many low-velocity purchases can be less than the KE value of their combined velocity.. again, ½mV² fixes the minimum unit-energy cost of accelerating 1 kg by 1 m/s to ½ J; repeat that 10x and you have 1 kg @ 10 m/s = 50 J, for a net outlay of 10 * 0.5 J = 5 J or ten times unity. These are obvs the maths to be playing with.
Begun playing around in WM today; two pendulums with variable MoI's, hanging outwards radially, counter-balanced against gravity while swinging under CF force.
Basically i want to pump their swings using the ice-skater effect, but instead of simply spinning-and-braking to scoop up momentum and dump it into the main wheel axis (per previous attempts), i plan to progressively raise GPE in the form of overbalancing weight. So the system will only actually be accelerated by OB torque; the momentum gains transferred to the OB system which involves a rotating aspect such as any of those presented in my previous thread here, perhaps even reducing to something as simple as this:
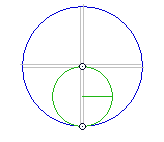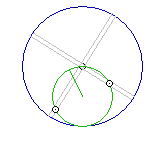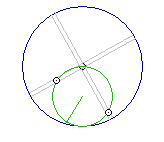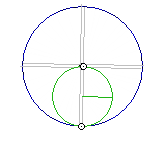
..so imagine something like that, the weight's rotation driven by pumping the swings of a pair of pendulums swinging under CF force. That's the aim; to sim it, then measure its efficiency..
@Trev - delta p over delta t, or change in momentum over change in time, like WaltzCee said - arguably the distinction between real and fictitious forces. Normally the ice-skater effect obviously trades inertia for velocity, for no net change in momentum. However it may be possible to fix that, via the principles i'm considering here; a reactionless rise in momentum being the singular action transitioning a system from unity minus losses to OU.
@WaltzCee - the maths of conservation obvs aren't 'wrong', but dependent on symmetries, esp. N3 / N1 concerning the conservation of momentum, and in turn, conservation of energy between velocity frames. Because energy squares with velocity, the sum of many low-velocity purchases can be less than the KE value of their combined velocity.. again, ½mV² fixes the minimum unit-energy cost of accelerating 1 kg by 1 m/s to ½ J; repeat that 10x and you have 1 kg @ 10 m/s = 50 J, for a net outlay of 10 * 0.5 J = 5 J or ten times unity. These are obvs the maths to be playing with.
Begun playing around in WM today; two pendulums with variable MoI's, hanging outwards radially, counter-balanced against gravity while swinging under CF force.
Basically i want to pump their swings using the ice-skater effect, but instead of simply spinning-and-braking to scoop up momentum and dump it into the main wheel axis (per previous attempts), i plan to progressively raise GPE in the form of overbalancing weight. So the system will only actually be accelerated by OB torque; the momentum gains transferred to the OB system which involves a rotating aspect such as any of those presented in my previous thread here, perhaps even reducing to something as simple as this:

..so imagine something like that, the weight's rotation driven by pumping the swings of a pair of pendulums swinging under CF force. That's the aim; to sim it, then measure its efficiency..
Last edited by MrVibrating on Sun Nov 05, 2023 12:28 am, edited 2 times in total.
Re: Mechanising the maths
The ice skater speeds up rotation, but doesn't add energy to the system. (I think).
Re: Mechanising the maths
.
.
You'll have ate your cake & have it 2. :)
.
obvs to you. Also if you were to be correct (but you are not), then the maths of conservation will be obliterated!@WaltzCee - the maths of conservation obvs aren't 'wrong', but dependent on symmetries, esp. N3 / N1 concerning the conservation of momentum, and in turn, conservation of energy between velocity frames. Because energy squares with velocity, the sum of many low-velocity purchases can be less than the KE value of their combined velocity.. again, ½mV² fixes the minimum unit-energy cost of accelerating 1 kg by 1 m/s to ½ J; repeat that 10x and you have 1 kg @ 10 m/s = 50 J, for a net outlay of 10 * 0.5 J = 5 J or ten times unity. [*]These are obvs the maths to be playing with.
You'll have ate your cake & have it 2. :)
........................¯\_(ツ)_/¯
¯\_(ツ)_/¯ the future is here ¯\_(ツ)_/¯
Advocate of God Almighty, maker of heaven and earth and redeemer of my soul.
Walter Clarkson
© 2023 Walter W. Clarkson, LLC
All rights reserved. Do not even quote me w/o my expressed written consent.
¯\_(ツ)_/¯ the future is here ¯\_(ツ)_/¯
Advocate of God Almighty, maker of heaven and earth and redeemer of my soul.
Walter Clarkson
© 2023 Walter W. Clarkson, LLC
All rights reserved. Do not even quote me w/o my expressed written consent.
-
MrVibrating
- Addict

- Posts: 2879
- Joined: Sat Jul 31, 2010 12:19 am
- Location: W3
-
MrVibrating
- Addict

- Posts: 2879
- Joined: Sat Jul 31, 2010 12:19 am
- Location: W3
Re: Mechanising the maths
KE=½mV², therefore it costs ½ J to accelerate 1 kg by 1 m/s from a standing start. If you can repeat that - buying the same 1 kg-m/s of momentum for the same ½ J - ten times on the trot (ie. implying a divergent inertial frame), then you've spent 10 * ½ J = 5 J, yet you now have 1 kg at 10 m/s hence 50 J of KE, or ten times unity.WaltzCee wrote: ↑Sun Nov 05, 2023 4:10 pm .
.obvs to you. Also if you were to be correct (but you are not), then the maths of conservation will be obliterated!@WaltzCee - the maths of conservation obvs aren't 'wrong', but dependent on symmetries, esp. N3 / N1 concerning the conservation of momentum, and in turn, conservation of energy between velocity frames. Because energy squares with velocity, the sum of many low-velocity purchases can be less than the KE value of their combined velocity.. again, ½mV² fixes the minimum unit-energy cost of accelerating 1 kg by 1 m/s to ½ J; repeat that 10x and you have 1 kg @ 10 m/s = 50 J, for a net outlay of 10 * 0.5 J = 5 J or ten times unity. [*]These are obvs the maths to be playing with.
You'll have ate your cake & have it 2. :)
Working backwards from first principles (deductive logic), this is the only possible route to a solution; the only way out of the '1+1=3 ?' conundrum.
-
MrVibrating
- Addict

- Posts: 2879
- Joined: Sat Jul 31, 2010 12:19 am
- Location: W3
Re: Mechanising the maths
Spent some time this morning investigating which type of mechanism may be optimal for kiiking under CF, as opposed to gravity.
Under gravity, the simplest solution reduces to a balanced variable moment of inertia, plus an unbalanced weight:

However the counter angular momenta of these swings seems likely to interfere with smooth application of OB torque from the OB mechanism.
One obvious problem may be the counter-momenta from swinging these weights in the first place - clearly, if a linked pair swing in the same angular direction each phase, their combined counter-momenta will have a significant effect on accelerating and decelerating the wheel. But even with counterposed angular directions, there's still hefty exchanges of angular momentum:

From a 1 rad/s push-start and then left to coast, speed almost halves from the swings' MoI variation.
An additional issue is that in order to optimise the excursion / stroke length under CF force, the radius of these weighted vMoI's needs to be half the wheel radius; this in turn means that as the weights swing upwards, they may begin to encroach on the center, where CF diminishes potentially to zero. All else being equal, this is likely to result in chaotic sync between multiple sets of swinging members as the system attempts to relax into its max-MoI, min-KE state:

With two pairs of counterposed swings the RPM's are more stabilised, but one pair ends up hogging more momentum than the other.
It looks like things could be stabilised further by gearing the two pairs to force sync; besides, these are just passive swings without vMoI's - actively pumping them, and then harnessing the resulting inertial torques to accelerate the rolling OB system, will add another layer of regulation.
However there are many different ways of 'kiiking', which simply reduces to controlling I/O ±G-time symmetry; spending more time under gravity's constant acceleration than deceleration per cycle, albeit reactionlessly; without applying force or torque to an external inertia or ground.
One alternative method could be to attach a weight with a high MoI to the edge of the wheel via a motor, then, as the wheel lowers the OB weight, spin it up so that the counter-torque slows the descent, increasing positive G-time. When rising again decelerate or brake it, thus accelerating the lifting phase and cutting negative G-time. The weight's spin thus oscillates, spinning and braking as it rises and falls, and causing the wheel to gain momentum from G*t each GPE cycle. Here's what that looks like:

So from a 1 rad/s push-start, all further momentum is gained from G*t, via this up vs down time asymmetry. That's all kiiking really is - performing some workload to purchase momentum from G*t, in an otherwise closed system of interacting masses. 'Kiiking' = 'gaining statorless momentum'.
But what works well under real gravity isn't necessarily optimal when operating under CF force; hence why i suspect kiiking with a linear action may be the way to go here:

This seems objectively better, insofar as eliminating the unnecessary angular component of the weight's motion. A single vMoI could be cranking two or more masses in and out on opposite sides of the wheel, and with two such sets for a total of four weights, the two shared vMoI's could counter-rotate, further minimising stray counter angular momenta from interfering with the rolling OB operation.
So the next problem to be solved is the issue of a ratchet and pawl mechanism; suffice to say i don't intend to model the clunky vagaries of a real one, so much as to simulate a simplified one-way bearing - a conditional constraint that clutches when torqued in one direction, and slips in the other. Once that's sussed i'll be ready to string together a complete mechanism, using inertial torques from pumping CF swings to progressively accelerate the OB system..
Under gravity, the simplest solution reduces to a balanced variable moment of inertia, plus an unbalanced weight:

However the counter angular momenta of these swings seems likely to interfere with smooth application of OB torque from the OB mechanism.
One obvious problem may be the counter-momenta from swinging these weights in the first place - clearly, if a linked pair swing in the same angular direction each phase, their combined counter-momenta will have a significant effect on accelerating and decelerating the wheel. But even with counterposed angular directions, there's still hefty exchanges of angular momentum:

From a 1 rad/s push-start and then left to coast, speed almost halves from the swings' MoI variation.
An additional issue is that in order to optimise the excursion / stroke length under CF force, the radius of these weighted vMoI's needs to be half the wheel radius; this in turn means that as the weights swing upwards, they may begin to encroach on the center, where CF diminishes potentially to zero. All else being equal, this is likely to result in chaotic sync between multiple sets of swinging members as the system attempts to relax into its max-MoI, min-KE state:

With two pairs of counterposed swings the RPM's are more stabilised, but one pair ends up hogging more momentum than the other.
It looks like things could be stabilised further by gearing the two pairs to force sync; besides, these are just passive swings without vMoI's - actively pumping them, and then harnessing the resulting inertial torques to accelerate the rolling OB system, will add another layer of regulation.
However there are many different ways of 'kiiking', which simply reduces to controlling I/O ±G-time symmetry; spending more time under gravity's constant acceleration than deceleration per cycle, albeit reactionlessly; without applying force or torque to an external inertia or ground.
One alternative method could be to attach a weight with a high MoI to the edge of the wheel via a motor, then, as the wheel lowers the OB weight, spin it up so that the counter-torque slows the descent, increasing positive G-time. When rising again decelerate or brake it, thus accelerating the lifting phase and cutting negative G-time. The weight's spin thus oscillates, spinning and braking as it rises and falls, and causing the wheel to gain momentum from G*t each GPE cycle. Here's what that looks like:

So from a 1 rad/s push-start, all further momentum is gained from G*t, via this up vs down time asymmetry. That's all kiiking really is - performing some workload to purchase momentum from G*t, in an otherwise closed system of interacting masses. 'Kiiking' = 'gaining statorless momentum'.
But what works well under real gravity isn't necessarily optimal when operating under CF force; hence why i suspect kiiking with a linear action may be the way to go here:

This seems objectively better, insofar as eliminating the unnecessary angular component of the weight's motion. A single vMoI could be cranking two or more masses in and out on opposite sides of the wheel, and with two such sets for a total of four weights, the two shared vMoI's could counter-rotate, further minimising stray counter angular momenta from interfering with the rolling OB operation.
So the next problem to be solved is the issue of a ratchet and pawl mechanism; suffice to say i don't intend to model the clunky vagaries of a real one, so much as to simulate a simplified one-way bearing - a conditional constraint that clutches when torqued in one direction, and slips in the other. Once that's sussed i'll be ready to string together a complete mechanism, using inertial torques from pumping CF swings to progressively accelerate the OB system..
Last edited by MrVibrating on Sun Nov 05, 2023 4:41 pm, edited 1 time in total.
