Hypothesis .. Raising GPE without using Law of Levers ? ..
Moderator: scott
-
johannesbender
- Addict

- Posts: 2567
- Joined: Thu Apr 18, 2013 3:29 pm
- Location: not important
Re: Hypothesis .. Raising GPE without using Law of Levers ? ..
@Fletcher , i have not been feeling well for a couple of days and as a result have been ghosting around here for brief moments , i have looked and read and are following .
As far as i can follow the first leg , you have shown (in post Sat Nov 16, 2024 2:47 am) that the mass (B1) which is half the weight of A1 and pushed twice the distance of A1 vs a mass (A1) which is twice the weight of B1 going half the distance of B1 , that at the pause B1 has double the work done of A1 and has double the KE of A1 and B1 has double the velocity of A1 in the first "leg" of the sim , and the the force applied over the distance for A1 is 5N and the force applied for distance B1 is 5N .
As far as i can follow the first leg , you have shown (in post Sat Nov 16, 2024 2:47 am) that the mass (B1) which is half the weight of A1 and pushed twice the distance of A1 vs a mass (A1) which is twice the weight of B1 going half the distance of B1 , that at the pause B1 has double the work done of A1 and has double the KE of A1 and B1 has double the velocity of A1 in the first "leg" of the sim , and the the force applied over the distance for A1 is 5N and the force applied for distance B1 is 5N .
Its all relative.
Re: Hypothesis .. Raising GPE without using Law of Levers ? ..
Bonjour Fletcher,
Je partage l'avis de Jhon tous ces graphiques me donne le tournis, je n'ai pas votre niveau théorique!! #:>(
Hi Fletcher,
I share the opinion of Jhon all these graphs gives me the screw head, I do not have your theoretical level!! #:>(
Je partage l'avis de Jhon tous ces graphiques me donne le tournis, je n'ai pas votre niveau théorique!! #:>(
Hi Fletcher,
I share the opinion of Jhon all these graphs gives me the screw head, I do not have your theoretical level!! #:>(
Last edited by SHADOW on Sat Nov 16, 2024 11:06 am, edited 1 time in total.
La propriété, c'est le vol!
P.J. PROUDHON
P.J. PROUDHON
Re: Hypothesis .. Raising GPE without using Law of Levers ? ..
Here is what Copilot came up with the percentage difference:
n the last simulation, the Work Done (WD) was -5.391 Nm, and the Kinetic Energy (KE) was -3.514 J. To find the difference in Joules (J) as a percentage, we can use the formula:
In the last simulation, the Work Done (WD) was -5.391 Nm, and the Kinetic Energy (KE) was -3.514 J. To find the difference in Joules (J) as a percentage, we can use the formula:
Percentage Difference = ((WD - KE) / WD) * 100
Plugging in the values:
Percentage Difference = ((-5.391 - (-3.514)) / -5.391) * 100
Percentage Difference = (-1.877 / -5.391) * 100
Percentage Difference ≈ 34.81%
So, the difference in Joules in the last simulation is approximately 34.81%.
What goes around, comes around.
Re: Hypothesis .. Raising GPE without using Law of Levers ? ..
. This is no different than the “Roller Racers” where I said energy equivalence didn’t add up. A lot better example.Copilot: Yes, according to the simulation results shared in the thread, the mass B1, which is half the weight of A1 and pushed twice the distance, indeed showed double the work done, double the kinetic energy, and double the velocity compared to A1 in the first leg of the simulation. The force applied over the distance for both A1 and B1 was 5N1
What goes around, comes around.
Re: Hypothesis .. Raising GPE without using Law of Levers ? ..
Copilot: In Fletcher's setup, the missing kinetic energy is a key point of discussion. The discrepancy between the work done and the kinetic energy gained suggests that some energy might be lost due to factors like friction or other inefficiencies.
In the "Rolling Racers" setup, the missing element is not kinetic energy but rather the difference in how energy is distributed among the objects due to their varying moments of inertia. Each object has a different moment of inertia, which affects their rotational motion and the energy they have when they reach the flag. When they hit something at the flag, their kinetic energy would indeed be different due to their varying moments of inertia. However, when it comes to returning to the starting height, the potential energy required is the same for all objects, as it depends solely on their height and mass.
So, while Fletcher's setup highlights missing kinetic energy, the "Rolling Racers" setup emphasizes the differences in energy distribution due to the moment of inertia. You can watch the video and learn more about it here.
Last edited by daxwc on Sat Nov 16, 2024 12:25 pm, edited 1 time in total.
What goes around, comes around.
Re: Hypothesis .. Raising GPE without using Law of Levers ? ..
So I have a stupid question Fletcher. The SIM has no friction from sliding because you doubled the area contact? I know it says "no friction" on the display.
This analysis shows that the discrepancy in kinetic energy is a result of the velocity squared term in the kinetic energy equation. Hmm... correct?
This analysis shows that the discrepancy in kinetic energy is a result of the velocity squared term in the kinetic energy equation. Hmm... correct?
Last edited by daxwc on Sat Nov 16, 2024 12:18 pm, edited 2 times in total.
What goes around, comes around.
-
johannesbender
- Addict

- Posts: 2567
- Joined: Thu Apr 18, 2013 3:29 pm
- Location: not important
Re: Hypothesis .. Raising GPE without using Law of Levers ? ..
@Fletcher
(im using the absolute values , eg -5 = 5 , -24 = 24)
Okay second leg , you show work done does not equal the KE .
For the work energy theorem : W = Δ(KE) Work = Change(Delta) in Kinetic Energy , which is the difference of the initial Kinetic energy and the final Kinetic energy .
Leg 1 , the initial KE was 0 there was a change in KE of 3.380 and W done was 3.380 wich is correct since 3.380 - 0 = 3.380 .
Leg 2 , the final KE is 3.514 , and you show work done is 5.391 , so 1.877 difference .
I cant see what the inital values for leg 2 were ,to fast for my eyes :)
edited (worded wrong)
(im using the absolute values , eg -5 = 5 , -24 = 24)
Okay second leg , you show work done does not equal the KE .
For the work energy theorem : W = Δ(KE) Work = Change(Delta) in Kinetic Energy , which is the difference of the initial Kinetic energy and the final Kinetic energy .
Leg 1 , the initial KE was 0 there was a change in KE of 3.380 and W done was 3.380 wich is correct since 3.380 - 0 = 3.380 .
Leg 2 , the final KE is 3.514 , and you show work done is 5.391 , so 1.877 difference .
I cant see what the inital values for leg 2 were ,to fast for my eyes :)
edited (worded wrong)
Last edited by johannesbender on Sat Nov 16, 2024 12:35 pm, edited 1 time in total.
Its all relative.
Re: Hypothesis .. Raising GPE without using Law of Levers ? ..
Thanks for the inputs fellas .. best of luck for everyone's experiments and projects naturally ..
Rather than reply to each post individually I'll sort of incorporate them all into this post ..
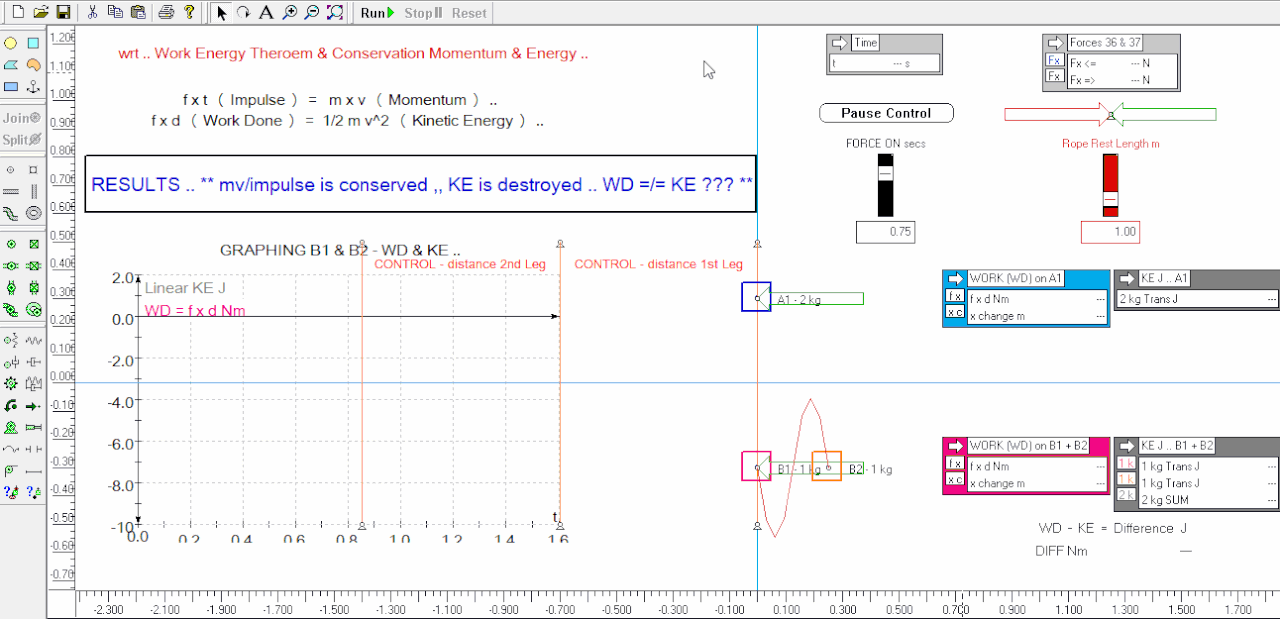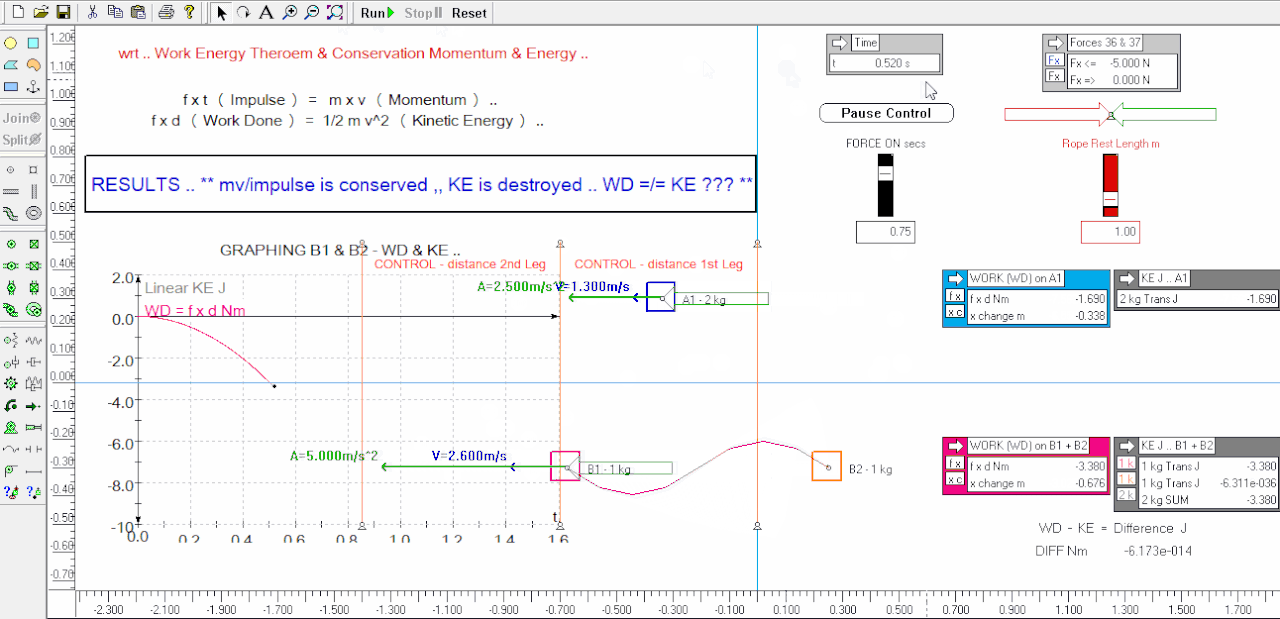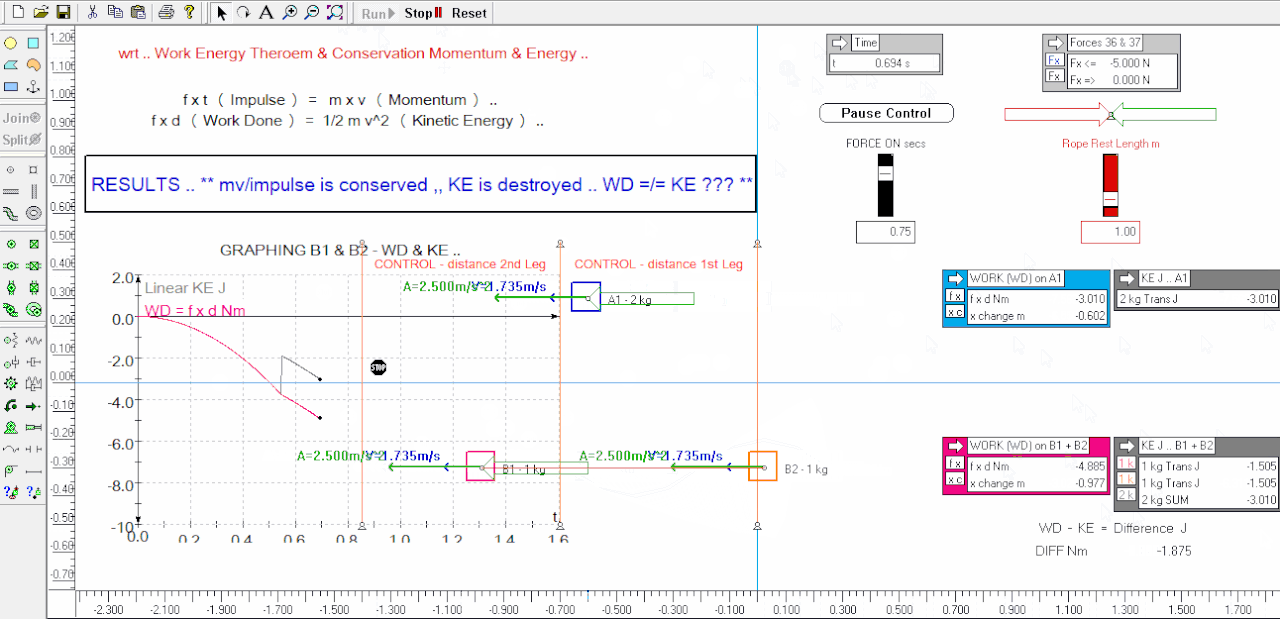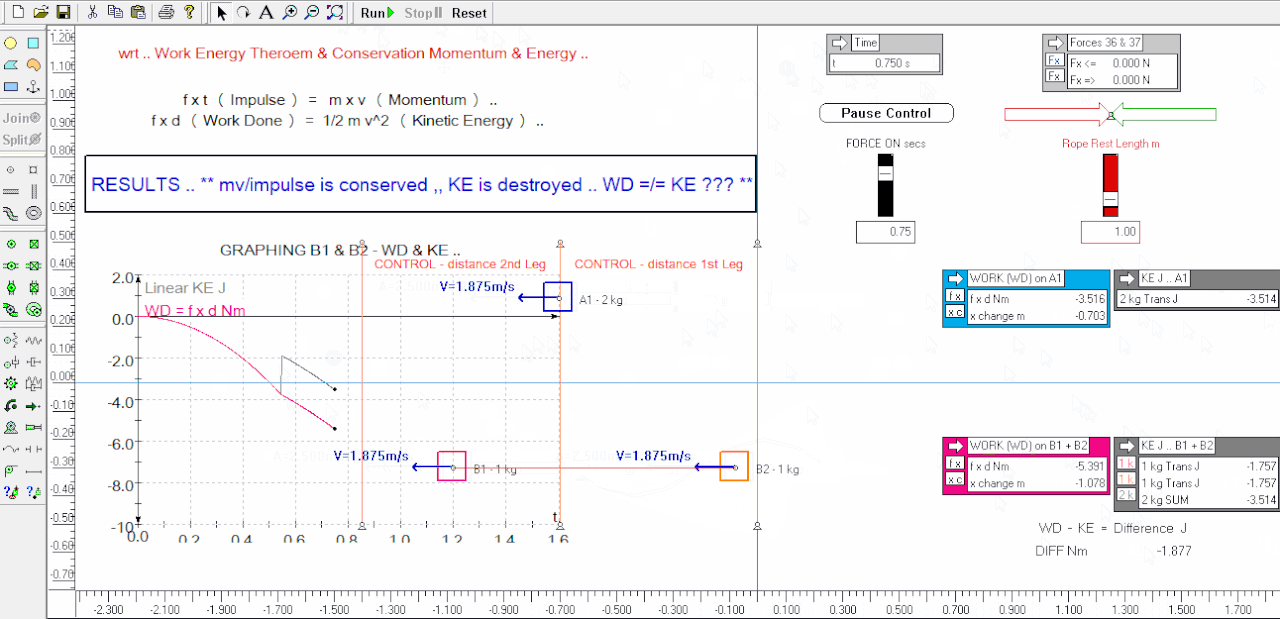
Here I redo the 'control vs ganged' experiment sim again - this time I labelled the distances the control travels during the 1st and 2nd legs of reversed impulse ( ft ) / momentum inputs - you can see visually and by the output tables that the horizontal distances are identical distances traveled for the 2 kg control .. also I added acceleration green vectors to the weights to make it easier too see the velocities are doubled for half the mass of the ganged sim B1 and that means the Momentum change is the same for both at any time interval etc .. I also halved the capture rate of the animation so I didn't have to zip around so fast in the time allowed which should be easier to follow ( can take a screen grab ) .. the 1st leg is split into ( paused at ) 2 parts as before - at 0.52 secs and again at 0.75 secs when the impulse / momentum given ceases - n.b. 2nd leg the impulse / momentum input is reversed as before but not shown in this animation ..
The sims have no frictions i.e. they are 'pure' experiments, with no friction energy losses to contact areas with slides, or air etc - but when the trailing B2 weight eventually collides with the B1 weight in leg 2 ( not shown in this animation grab ) they have elasticity set to 0.5 so there are energy losses at this stage due to deformation, synthesized heat and sound etc, of the objects etc - however this is AFTER the 1st leg we are examining here ..
................
................
The things imo of note is that the sims start from stationary i.e. have no momentum or energy .. in the 1st leg they are given an identical impulse ( f.t ) - iow's their momentums are changed by a consistent input of constant force x time - this is seen in the visuals and this time I did not include the output tables of the relative momentums ( at any time ) which are the same for both - however we can see that the ganged sim B1 has twice the acceleration of the A1 control, and twice the velocity, and twice the KE ( altho their momentum changes are the same ) - after the first pause at 0.52 secs the sim runs on to complete the 1st leg of impulse / momentum input .. at the instant the massless rope connecting B1 to B2 is tight the KE of B2 drops significantly ( see output tables ), and of course B2 gains momentum and KE - at this time momentum changes are still the same for both control and ganged experiment ..
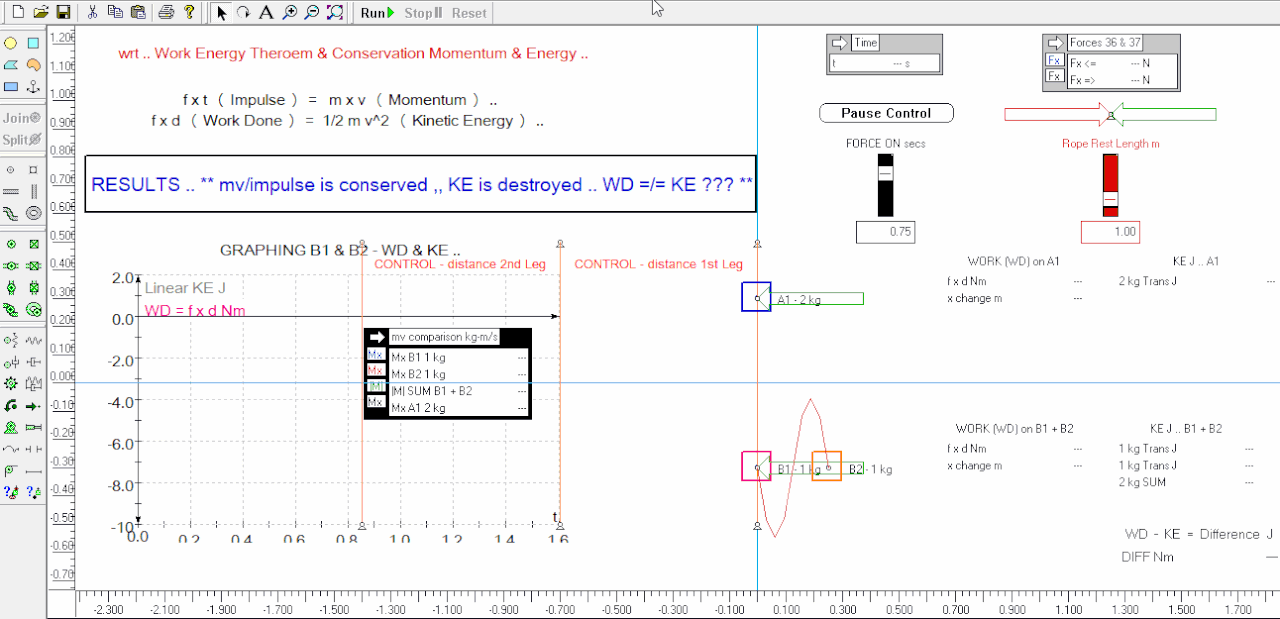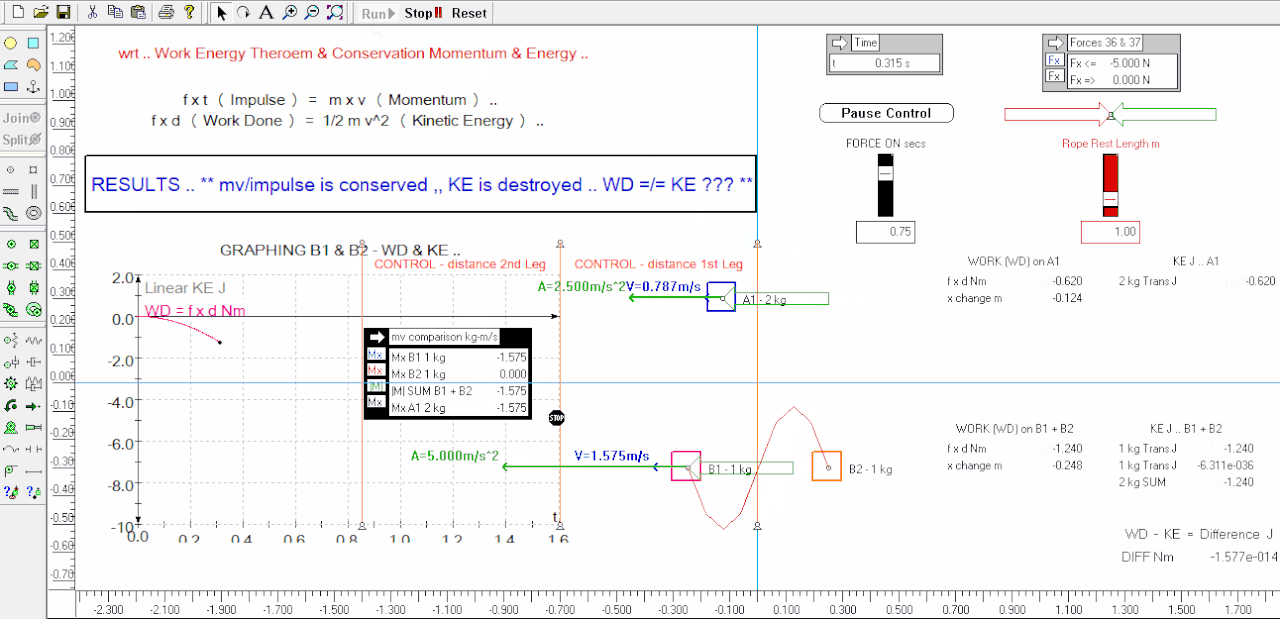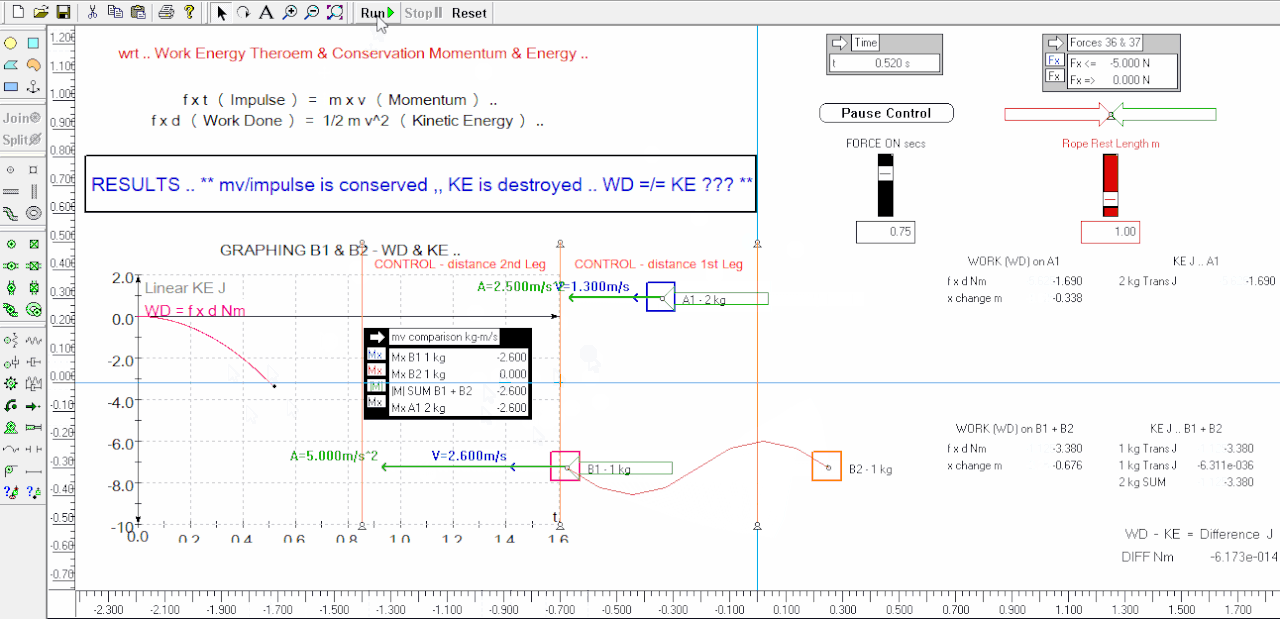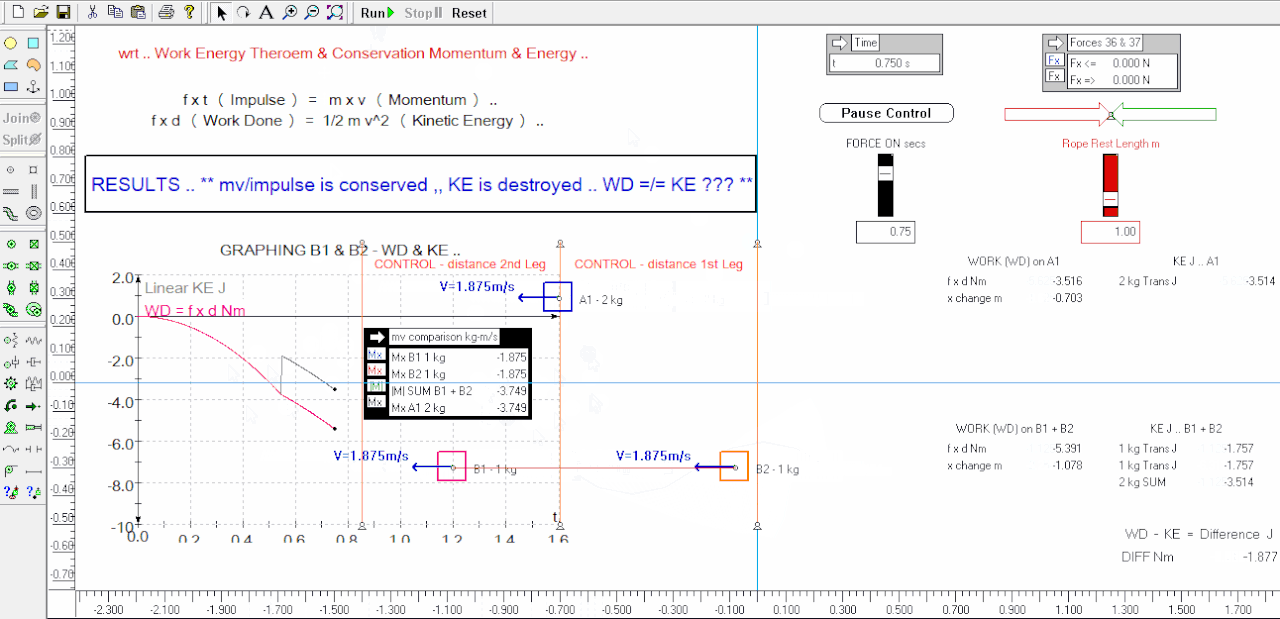
When we look at the graphs of the ganged experiment we can visually see that up until the rope went taut the WD ( f.d ) was equal to the KE of B1 - after the rope goes taut the 2 ganged weights KE added together was substantially less ( 34% less ) than the WD on the system at the end of the 1st leg at 0.75 secs - we are missing 1.87 Nm ( J ) or energy ( it is literally Missing In Action ) ALTHO the Work was Done ( it was paid for ) !
Here are my takeaways ..
Momentum is a vector ..
Energy is a scalar ( magnitude but no direction ) ..
At all and any slice in time you care to look at the momentum ( mv ) changes to both the control and the ganged system is identical and consistent with fundamental Conservation of Momentum .. this mv change consistency holds right thru legs 1 and 2 at any identical time slice ..
My summary of what is happening in the 1st leg example to the ganged experiment ..
1. momentum ( mv ) is "spent" on the system in the time allotted via the impulse given, and the mv accumulates ..
2. a set amount of 'Work is done' in this time allowed i.e. Work ( f x d ) is literally "spent/banked" on increasing the momentums and by default the weights 'energy' ( re Work Energy Equivalence ) ..
3. the weights conserve the momentum changes ! ..
4. the weights register a given and consistent set amount of energy ( KE ) and this has symmetry until the rope goes tight ..
>>>
5. after the rope goes tight ( n.b. no energy losses to the rope in the sim ) we have a significant shortfall in "energy" when we compare the WD right up to 0.75 secs, to the sum of the B1 + B2 ganged weights KE .. ( see the graph of WD against summed KE )
6. some "energy" is not registering in the sim - we have KE but in layman's terms some 'energy' mysteriously has "evaporated" or been transformed into some other type not being metered - i.e. it is missing/gone on holiday it appears ..
7. this MIA energy to WD invested will also be a scalar quantity having magnitude but not direction - it appeared plausible to me that rather than have it go unaccounted for then it could be mechanically induced to reappear in a potentially useful form we can both see and use such as PE increase, with another entirely different arrangement - and potentially perhaps also balance the energy budget and reinstate the Work Energy Theorem ..
..............
More sim scenario's to eventually follow once I dust them off and have time ..
Rather than reply to each post individually I'll sort of incorporate them all into this post ..
Here I redo the 'control vs ganged' experiment sim again - this time I labelled the distances the control travels during the 1st and 2nd legs of reversed impulse ( ft ) / momentum inputs - you can see visually and by the output tables that the horizontal distances are identical distances traveled for the 2 kg control .. also I added acceleration green vectors to the weights to make it easier too see the velocities are doubled for half the mass of the ganged sim B1 and that means the Momentum change is the same for both at any time interval etc .. I also halved the capture rate of the animation so I didn't have to zip around so fast in the time allowed which should be easier to follow ( can take a screen grab ) .. the 1st leg is split into ( paused at ) 2 parts as before - at 0.52 secs and again at 0.75 secs when the impulse / momentum given ceases - n.b. 2nd leg the impulse / momentum input is reversed as before but not shown in this animation ..
The sims have no frictions i.e. they are 'pure' experiments, with no friction energy losses to contact areas with slides, or air etc - but when the trailing B2 weight eventually collides with the B1 weight in leg 2 ( not shown in this animation grab ) they have elasticity set to 0.5 so there are energy losses at this stage due to deformation, synthesized heat and sound etc, of the objects etc - however this is AFTER the 1st leg we are examining here ..
................

................
The things imo of note is that the sims start from stationary i.e. have no momentum or energy .. in the 1st leg they are given an identical impulse ( f.t ) - iow's their momentums are changed by a consistent input of constant force x time - this is seen in the visuals and this time I did not include the output tables of the relative momentums ( at any time ) which are the same for both - however we can see that the ganged sim B1 has twice the acceleration of the A1 control, and twice the velocity, and twice the KE ( altho their momentum changes are the same ) - after the first pause at 0.52 secs the sim runs on to complete the 1st leg of impulse / momentum input .. at the instant the massless rope connecting B1 to B2 is tight the KE of B2 drops significantly ( see output tables ), and of course B2 gains momentum and KE - at this time momentum changes are still the same for both control and ganged experiment ..
When we look at the graphs of the ganged experiment we can visually see that up until the rope went taut the WD ( f.d ) was equal to the KE of B1 - after the rope goes taut the 2 ganged weights KE added together was substantially less ( 34% less ) than the WD on the system at the end of the 1st leg at 0.75 secs - we are missing 1.87 Nm ( J ) or energy ( it is literally Missing In Action ) ALTHO the Work was Done ( it was paid for ) !
Here are my takeaways ..
Momentum is a vector ..
Energy is a scalar ( magnitude but no direction ) ..
At all and any slice in time you care to look at the momentum ( mv ) changes to both the control and the ganged system is identical and consistent with fundamental Conservation of Momentum .. this mv change consistency holds right thru legs 1 and 2 at any identical time slice ..
My summary of what is happening in the 1st leg example to the ganged experiment ..
1. momentum ( mv ) is "spent" on the system in the time allotted via the impulse given, and the mv accumulates ..
2. a set amount of 'Work is done' in this time allowed i.e. Work ( f x d ) is literally "spent/banked" on increasing the momentums and by default the weights 'energy' ( re Work Energy Equivalence ) ..
3. the weights conserve the momentum changes ! ..
4. the weights register a given and consistent set amount of energy ( KE ) and this has symmetry until the rope goes tight ..
>>>
5. after the rope goes tight ( n.b. no energy losses to the rope in the sim ) we have a significant shortfall in "energy" when we compare the WD right up to 0.75 secs, to the sum of the B1 + B2 ganged weights KE .. ( see the graph of WD against summed KE )
6. some "energy" is not registering in the sim - we have KE but in layman's terms some 'energy' mysteriously has "evaporated" or been transformed into some other type not being metered - i.e. it is missing/gone on holiday it appears ..
7. this MIA energy to WD invested will also be a scalar quantity having magnitude but not direction - it appeared plausible to me that rather than have it go unaccounted for then it could be mechanically induced to reappear in a potentially useful form we can both see and use such as PE increase, with another entirely different arrangement - and potentially perhaps also balance the energy budget and reinstate the Work Energy Theorem ..
..............
More sim scenario's to eventually follow once I dust them off and have time ..
Last edited by Fletcher on Sun Nov 17, 2024 10:38 pm, edited 1 time in total.
Re: Hypothesis .. Raising GPE without using Law of Levers ? ..
Nice work Fletcher. I don't like Copilots answer but it does give it some color. I wonder how the SIM handles rope deformation. The problem with Algodoo is that part of the SIM sucks as it makes a bunch of segments with errors.Copilot: From my first impressions, it seems like Fletcher has put a lot of thought into his experiments and simulations. However, there might be a few areas where the logic could be further examined:
Energy Conservation: Fletcher mentions that the work done (WD) is greater than the kinetic energy (KE) gained, suggesting that some energy is "missing." This discrepancy could be due to the fact that energy is being transformed into other forms, such as heat or sound, which are not accounted for in the simulation.
Rotational Kinetic Energy: When the rope connecting B1 and B2 goes taut, the kinetic energy of B2 drops significantly, and B2 gains momentum and KE. This suggests that some energy is being transferred between the two masses, but not all of it is being accounted for in the form of kinetic energy.
Work-Energy Theorem: The work-energy theorem states that the work done on an object is equal to the change in its kinetic energy. In Fletcher's simulations, the work done seems to be greater than the kinetic energy gained, suggesting that some energy is not being accounted for.
Potential Energy Increase: Fletcher suggests that the missing energy could be mechanically induced to reappear in a useful form, such as an increase in potential energy. This could help balance the energy budget and reinstate the work-energy theorem.
Overall, Fletcher's analysis is insightful, but it might benefit from a closer examination of the energy transformations and distributions in the system. The missing energy could be due to factors like friction, deformation, or other inefficiencies that are not accounted for in the simulation.
Anyway I still think it is the squaring of velocity.
In the following video they aren't sure energy is conserved in all situations. They made energy conservative to fulfill their ledger on a short cut.
https://www.youtube.com/watch?v=Q10_srZ-pbs
Last edited by daxwc on Mon Nov 18, 2024 11:51 am, edited 1 time in total.
What goes around, comes around.
-
johannesbender
- Addict

- Posts: 2567
- Joined: Thu Apr 18, 2013 3:29 pm
- Location: not important
Re: Hypothesis .. Raising GPE without using Law of Levers ? ..
It appears the discrepancy in your gif of the sim happens around 0.548 s (sim time) , up to that time everything is fine , i made a screen shot and recorded a gif so may see the exact moment.
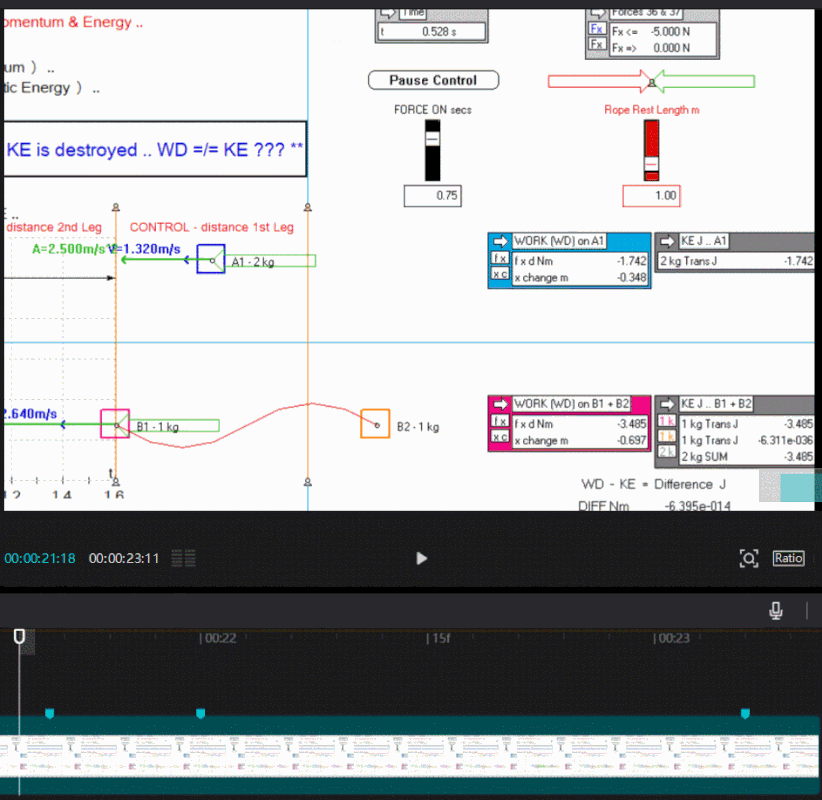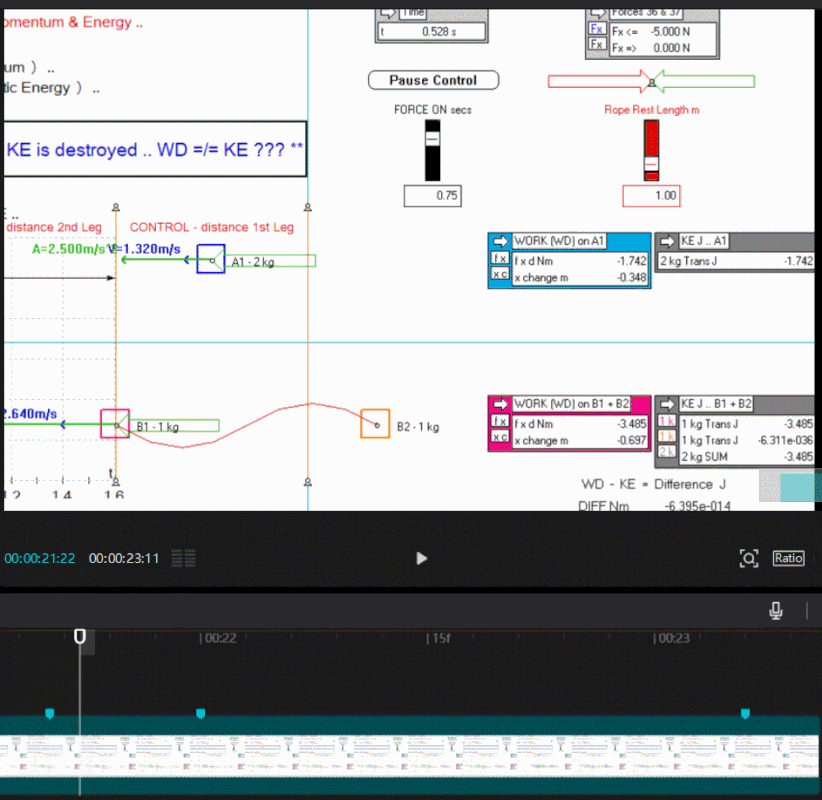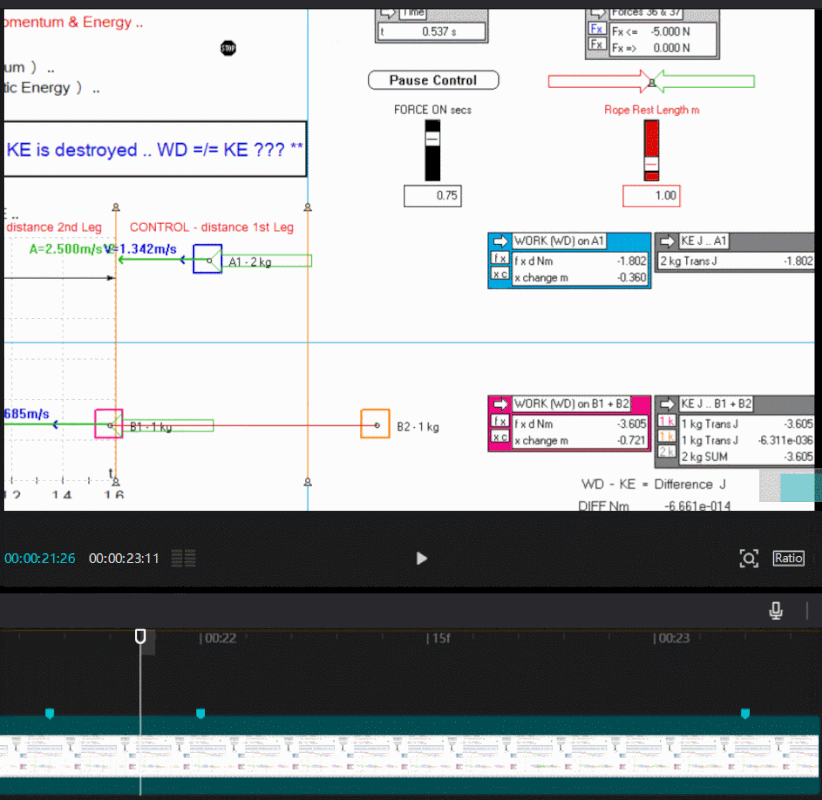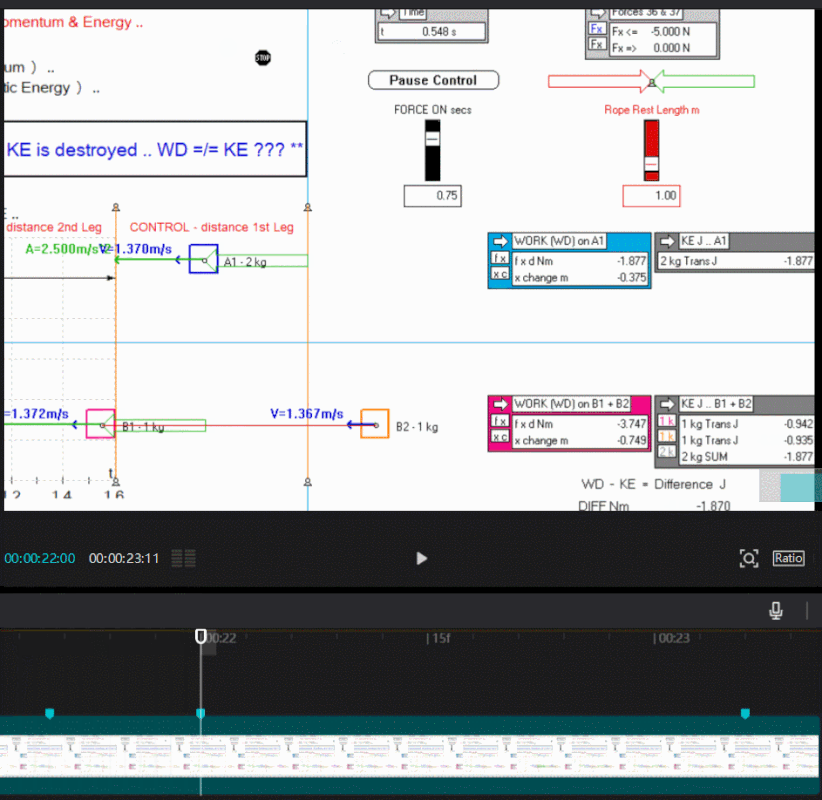

Its all relative.
Re: Hypothesis .. Raising GPE without using Law of Levers ? ..
Cheers jb .. maybe my explanation below will help fill in the picture a bit more .. no discrepancy as far as I can tell, just a transition phase ..jb wrote:It appears the discrepancy in your gif of the sim happens around 0.548 s (sim time) , up to that time everything is fine , i made a screen shot and recorded a gif so may see the exact moment.
I think it helps to look at these experiments in terms of Cause and Effect ..daxwc wrote:
I wonder how the SIM handles rope deformation. The problem with Algodoo is that part of the SIM sucks as it makes a bunch of segments with errors.
It doesn't handle rope deformation dax - its just a link from B1 to B2 - I could have replaced it with a stiff spring for example and we would see it's length slightly wax and wane until it quickly settled to rest length - this would show the momentums and energy's also waxing and waning slightly but it is not material to the exercise ( see below comments ) - in the real-world both a spring and a rope would have some very small energy losses to deformation and heat etc .. the sim is "pure" to show "pure relationships" for this straight forward linear experimental comparison ..
Anyway I still think it is the squaring of velocity.
As we've talked about previously mv ( momentum ) and 1/2mv^2 ( kinetic energy ) are different faces of the same coin - both can be mathematically calculated from knowing the velocity at any point in time - because I made the B1 wt 1/2 the A1 wt then it keeps things simple - we see the velocity is doubled, the ke is doubled ( because of v^2 ) for the same inputs of momentum change - ** how I propose to physically change the momentums will branch off this discussion further down the track I imagine ..
See comments below ..
............
In the following video they aren't sure energy is conserved in all situations. They made energy conservative to fulfill their ledger on a short cut.
https://www.youtube.com/watch?v=Q10_srZ-pbs
Good video dax, I enjoyed it ..
The compared experiments are given a known and equal input of momentum change during leg 1 .. ** momentum change is the currency in the experiment to change movement ..
The sim is paused at 2 steps in leg 1 - at all times in leg 1 the linear momentums for both the control experiment and the comparison experiment are identical i.e. they both gain the same linear momentum .. see animation below which has a black output in the graph section comparing one above the other the momentums to time during the 1st leg ..
While and when the change to momentums is performed it is said that we can also at any time period calculate and predict the objects KE - thru the Work Energy Theorem we can calculate the Work Done ( f x d in N.m) and this will give us the objects subject to movement KE's in Joules ..
** Classical Physics is a circular referencing system i.e. if you know 1 or 2 things you can find one face or the other face of the same coin .. because it is a closed system, with circular referencing, it also means that the relationships between momentum changes to the system, Work Done on the system, and Energy changes to the system are not plastic or fluid i.e. they have perfect symmetry circling back to the conservation laws for momentum and energy ( and Newton's Laws ) ..
In this example the WD does not always equal the summed KE of B1 + B2 in the comparison experiment ( altho both received the same input of momentum change ) vividly shown after the rope is drawn taut and onwards to the 0.75 second mark ..
** Energy is scalar and is the "Capacity to do Work' - Energy is the currency for doing Work - about the 0.548 second mark we lose about 34% of our currency to do Work i.e. lose our ability to perform Work - the Work Done ( f x d ) on the system was "spent" i.e. a sunk cost - the 'sunk' WD is far in excess of the available KE to do Work i.e. an analogy would be we have sunk $100 into moving our system, but we get only $66 back on our investment to do Work - this seems a bad deal, and appears to throw classical physics symmetry, and the Work Energy Theorem out the door ..
But hold on .. maybe we don't need to, or it is wrong to, throw the baby out with the bath water, and in this simple experiment we are more correctly just not efficiently using ALL the 'sunk' WD ( energy ) - we know we have a lesser amount than WD of KE available to do Work ( this is heresy and disruptor thought ) - perhaps we can use the rest of the sunk WD which we don't capture as KE to create GPE ( potential energy ) ? - and balance the books - energy is scalar after all, and is a measure of ability to do Work - GPE is energy ..
.............
.............
-
johannesbender
- Addict

- Posts: 2567
- Joined: Thu Apr 18, 2013 3:29 pm
- Location: not important
Re: Hypothesis .. Raising GPE without using Law of Levers ? ..
The point i was trying to make is it happens around the mark after the rope tightens , as for an explanation - i personally dont have an explanation which i can visually show , i changed the rope for a rod that becomes active when B1 reaches 0.7meters and the result is the same , my suspicion is it could be something that happens internally at the moment B1 starts tugging and onwards (The issue is i have no idea if thats true) .
chatgpt wrote something similar with the result i gave it (it has no other explanation too):
chatgpt wrote something similar with the result i gave it (it has no other explanation too):
I wondered if you could do it in the vertical eg. pulling B1 up which then tugs up B2 (perhaps later if you want to).Even with a massless, rigid rod:
The force dynamics still create an internal energy redistribution.
The total energy input (5.255J) includes work done that doesn't directly increase the kinetic energy of the objects.
This behavior is a consequence of the constraint force exerted by the rod. While the rod doesn't store energy, the force it transmits temporarily "redirects" energy in a non-kinetic form during the motion transfer.
Last edited by johannesbender on Tue Nov 19, 2024 11:58 am, edited 1 time in total.
Its all relative.
Re: Hypothesis .. Raising GPE without using Law of Levers ? ..
That is fine, but in classical physics, if the energy didn't come out as kinetic energy, then it must reside in the closed system as potential energy (PE) because energy cannot be created or destroyed. So the obvious question in your SIM example is: where is this missing energy physically? :)Fletcher: But hold on .. maybe we don't need to, or it is wrong to, throw the baby out with the bath water, and in this simple experiment we are more correctly just not efficiently using ALL the 'sunk' WD ( energy ) - we know we have a lesser amount than WD of KE available to do Work ( this is heresy and disruptor thought ) - perhaps we can use the rest of the sunk WD which we don't capture as KE to create GPE ( potential energy ) ? - and balance the books - energy is scalar after all, and is a measure of ability to do Work - GPE is energy ..
Last edited by daxwc on Tue Nov 19, 2024 12:13 pm, edited 1 time in total.
What goes around, comes around.
-
johannesbender
- Addict

- Posts: 2567
- Joined: Thu Apr 18, 2013 3:29 pm
- Location: not important
Re: Hypothesis .. Raising GPE without using Law of Levers ? ..
@Fletcher afai can see , the rod measures around -6 watts on activation for a small period of time .
Its all relative.
Re: Hypothesis .. Raising GPE without using Law of Levers ? ..
johannesbender wrote:
... i changed the rope for a rod that becomes active when B1 reaches 0.7meters and the result is the same , my suspicion is it could be something that happens internally at the moment B1 starts tugging and onwards (The issue is i have no idea if thats true) ...
All very good questions guys ..daxwc wrote:That is fine, but in classical physics, if the energy didn't come out as kinetic energy, then it must reside in the closed system as potential energy (PE) because energy cannot be created or destroyed.Fletcher: But hold on .. maybe we don't need to, or it is wrong to, throw the baby out with the bath water, and in this simple experiment we are more correctly just not efficiently using ALL the 'sunk' WD ( energy ) - we know we have a lesser amount than WD of KE available to do Work ( this is heresy and disruptor thought ) - perhaps we can use the rest of the sunk WD which we don't capture as KE to create GPE ( potential energy ) ? - and balance the books - energy is scalar after all, and is a measure of ability to do Work - GPE is energy ..
So the obvious question in your SIM example is: where is this missing energy physically? :)
The sim program is built on Classical Physics ( and the math ) - it does what it does, and predicts what it predicts - if you know some classical physics and keep the sim simple then you are in a position to test it and try and catch it out ( chinks-in-the-armour of Classical Physics symmetry, loopholes and/or workarounds ) - this is what I was doing with this and similar sims way back when ..
From these examples, and similar, it firmed up in my mind that Conservation of Momentum is the most fundamental of the Laws - and I would expect that actually - since momentum is just mv or ft - so if you start from that premise then the results actually makes sense imo - we give the sims mv - the masses have inertia and they steadily increase their velocities to reflect the impulse/momentum input to them - for the single weight control A1 experiment everything conforms nicely to Conservation of Momentum and Conservation of Energy Laws - the impulse given is tracked as Momentum gain and Kinetic gain - job done - symmetry holding ..
In the ganged B1 and B2 weights comparison experiment things apparently begin to go awry - it's all fine and dandy until the ( energy lossless ) rope/rod goes tight - we have ponied-up ( WD = fd ) to cause a movement and up until that moment the sim predicted symmetry and full accountability of the Laws of Conservation of Momentum and Energy - tick ! ..
After B2 gets tugged along ( it started its movement much later than B1 i.e. a time consideration ) we apparently no longer have all the previous energy/capacity available to do Work >> but the sim is what it is, and what it predicts >> there are no energy losses to frictions or deformations etc ..
So it begged the question to me - what was the more fundamental Conservation Law based on this thought experiment and simulation exercise ? .. for me Conservation of Momentum, because whether the control or the ganged pull along experiment, the mv changes from the identical impulses given were lock-stepped and the same for both at any time slice, right to the end of the 1st leg which included the pull along action ..
And if mv change was consistent and lock-stepped for both experiments then the KE must drop significantly once B1 and B2 had the same velocities as A1 after the rope goes tight ..
If the sum of the KE's of B1 and B2 after the pull-along had equaled the actual WD ( as Work Energy Theorem tells us it should, and Conservation of Energy Law ) then their velocities after the pull-along MUST BE much higher ( not all equal ) - therefore at that point in the time line they would also have greater momentum than given by the impulse ( ft ) up to that time stamp ..
Devils in the detail .. so I go back to my previous thought - Conservation of Momentum is the more fundamental Law - however, to validate Work Energy Equivalence Theorem ( symmetry ) when a "simple" sim built on Classical Physics has no ( and can not have ) energy losses, then for this 'linear' example to also Conserve ALL Energy, and where the WD does not equal the KE, then there is a unrealized capacity to do Work ( PE ) - i.e. the simple demonstration and testing sim experiment lacks the design-finesse to capture GPE to balance the Conservation of Energy books, imo ..
