Hypothesis .. Raising GPE without using Law of Levers ? ..

[daxwc]

Sorry Fletcher. I didn’t mean for you to make such a long retort. It was simply a statement, more about the Algodoo program, where you can see it is correcting to PE of the object. It was just frustration as to how people expect to find any overunity in a system that is designed to take it out.

Don’t get me wrong it is a great tool.

[Fletcher]

No probs dax -- and a great segue ..

It is exactly why a few of us repeatedly say that the only way to ' beat the system ' is to ' work with the system ' - find a mechanical workaround to physically lift weights and restore GPE of weights on the " cheap " i.e. discounted or next to no " energy " cost of lifting lol ..

I say under my breath " you got to cheat the system to beat the system " ..

[thx4]

Réflexion idéologique 🙂
Je pense qu'il n'y a pas de poids à monter...
A une certaine vitesse ( on suppose des poids en périphérie de la roue), les poids ne pèsent plus rien du tout...
Je pense que c'est compris lol, il suffirait d'un micro-freinage pour voir les poids reprendre le travail, et si la maquette est bien faite, les poids ne pourraient changer de position marquante que d'un coté. Micro-accélération/Micro-freinage. Micro-accélération/Micro-freinage 👽 . Le tout à travers un disque d'insertie qui va plus vite que le moteur de base.

Ideological thinking 🙂
I think there are no weights to mount....
At a certain speed ( we assume weights on the periphery of the wheel), the weights don't weigh anything at all....
I think that's understood lol, it would only take a micro-braking to see the weights take up the work again, and if the model is well made, the weights could only change their prominent position on one side. Micro-acceleration/Micro-braking. Micro-acceleration/Micro-braking 👽All through an insertie disk that goes faster than the basic motor.

[thx4]

:-) actually you are quite funny.
Let me try to explain why the brake is energy.
- when you brake it this way, (by locking the pendulum at the top of the flywheel and turning the flywheel) the cost of lifting the pendulum is the same as if you did it without a flywheel.
When you change the direction of the potential energy and actually - MOVE THE POTENTIAL ENERGY - to the flywheel, the flywheel got longer distance to its axis of its turning point so - it got a higher momentum.
This relationship is between those two potentials - it’s the difference between those two that drives the wheel not gravity.

Ideological thinking 🙂
I think there are no weights to mount....
At a certain speed ( we assume weights on the periphery of the wheel), the weights don't weigh anything at all....
I think that's understood lol, it would only take a micro-braking to see the weights take up the work again, and if the model is well made, the weights could only change their prominent position on one side. Micro-acceleration/Micro-braking. Micro-acceleration/Micro-braking 👽All through an inertie disk that goes faster than the basic motor.

Hi Frog,
I'm following you a bit more but your explanation is a bit long in coming
tell me if what you're thinking is close to what I'm trying to explain in this post above?

[thx4]

sorry little error of direction...
impossible to delete a post !!!

[Fletcher]

.. Bump ..

Thought I'd be able to get a sim animation up today of my "free lifting experiment" with a discussion of it to get things back on track in my topic - but things have conspired against me this morning - maybe later ..

Anyways .. I'm sure the sim experiment will be thought provoking for most - imo we will need all our critical thinking skills to logically agree on what it means ..

[Fletcher]

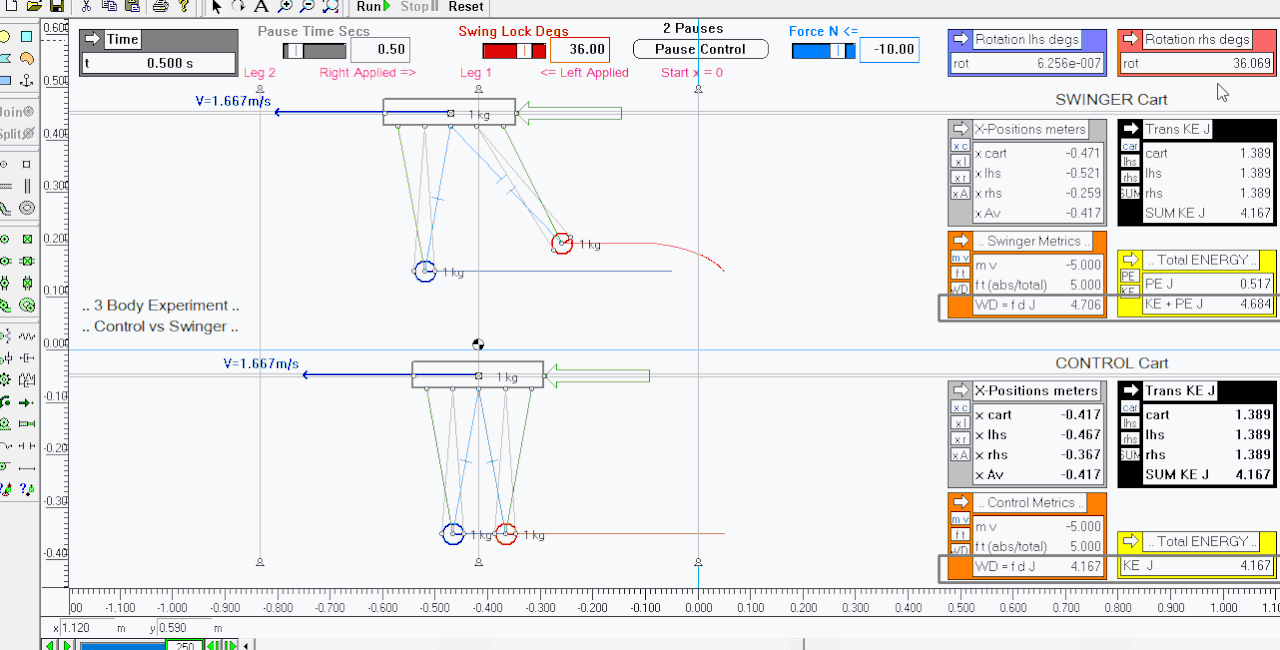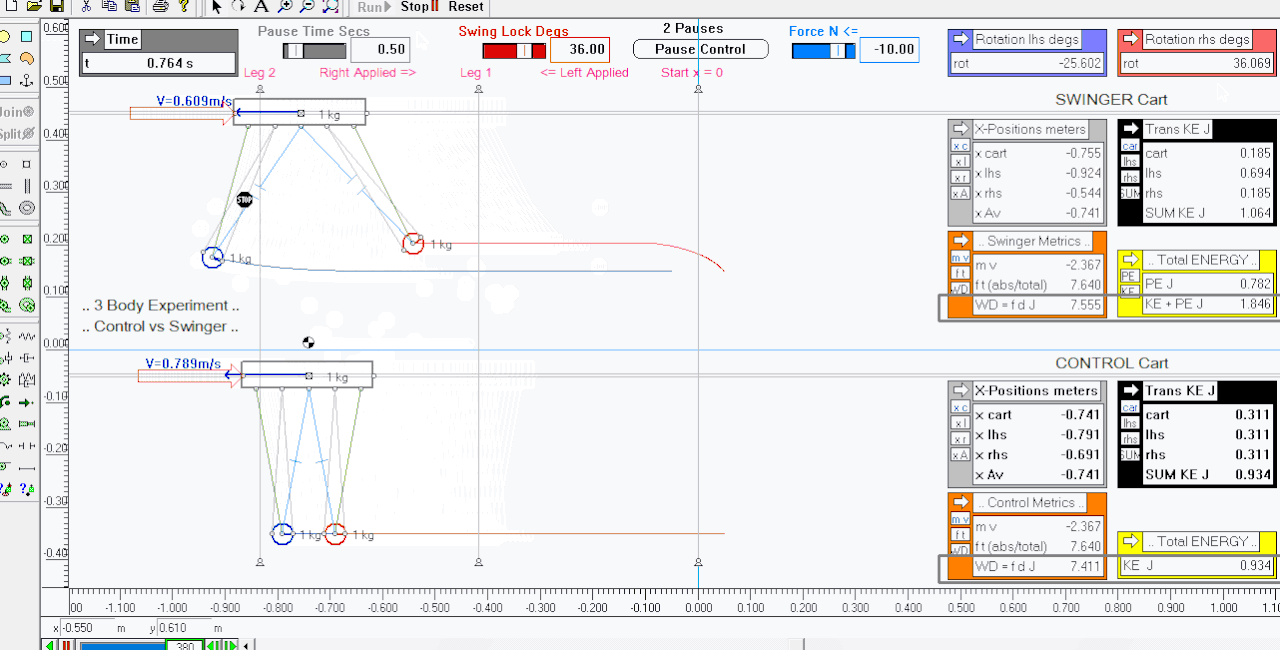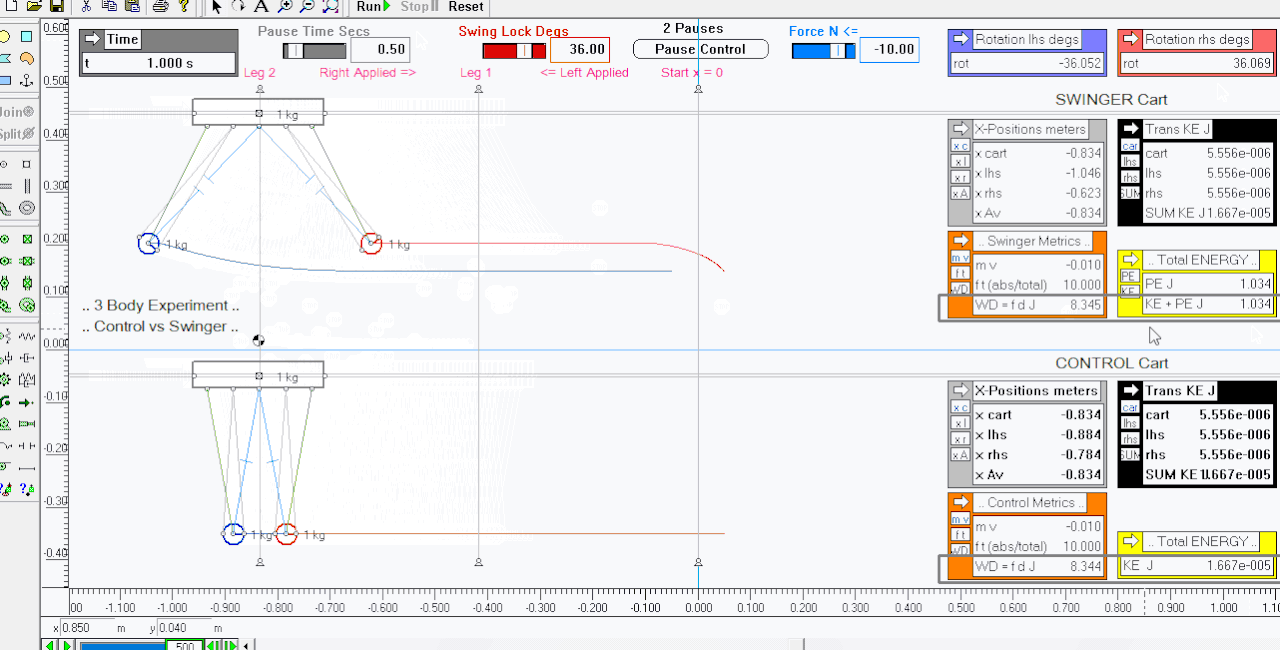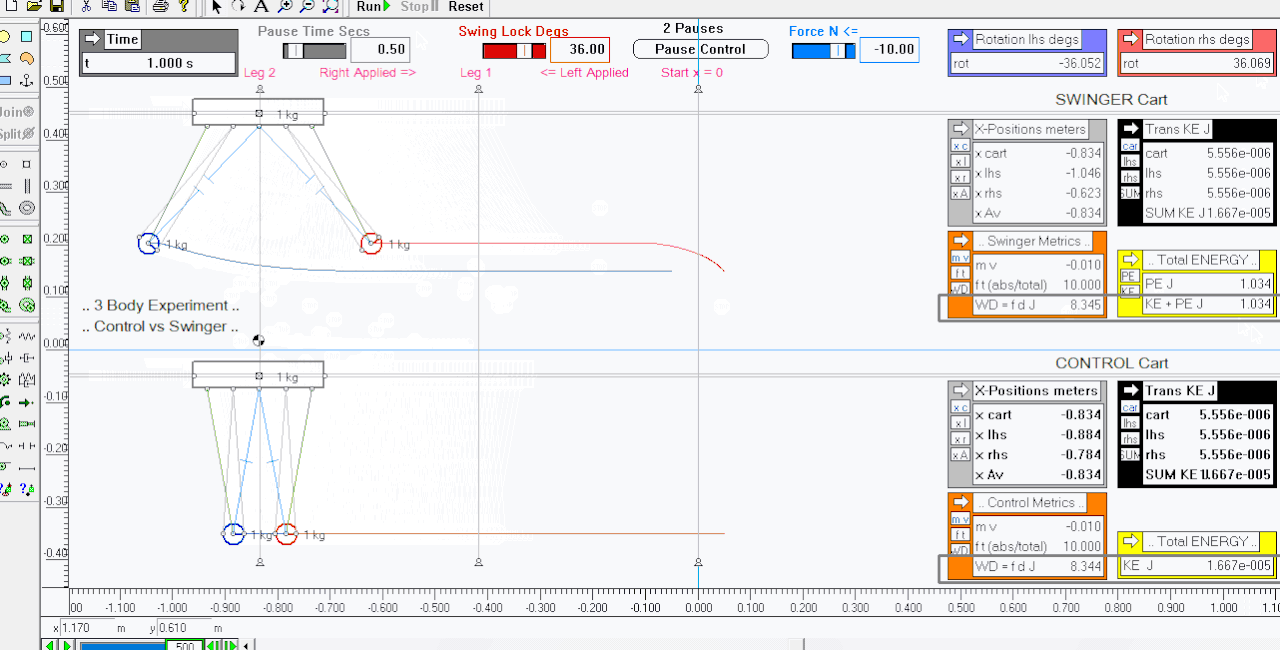
Here is the first leg of my free-lifting sim experiment ..

I have simplified the sim Output and Metrics as much as I can so most can follow the important ones in the animation and pics ..

...............

The experiment explores two identical carts able to move horizontally ( from a standing start ) - i.e. the Control Cart ( bottom ) and the Swinger Cart ( top ) .. the Control is rigid and the hanging pendulums unable to swing ( all one-piece ) - the Swinger has free to swing pendulums but only when the lock mechanism allows, dependent on direction free to swing ..

The source of change in movement to the carts is an injection of Impulse, which as we know is a change in Momentum because ft = mv from earlier discussions in this thread .. ** it is important to note that a change in momentum can happen at any cart starting momentum as per Newton's Laws - an Impulse will simply change its momentum from what it currently is ..

The carts are given an Impulse of 10 N's for 0.5 secs to the left at which time the sim is paused - this is the end of Leg 1 .. for Leg 2 the Impulse is reversed i.e. 10 N's for 0.5 secs in the reverse direction .. yet to be shown ..

................

Things to notice ..

The control cart travels 0.417 meters to the left and at the end of leg 1 has 1.667 m/s velocity - it had a momentum change of 5.000 kg.m/s ( 5.000 N.secs ) - it gained translation KE of 4.167 J - had 0.000 J PE gain or loss - therefore had total Energy gain of 4.167 J - the Work Done ( f x d ) was 4.167 J matching the KE gained ** WEEP is consistent ..

The swinger cart ( just the cart where force is applied ) travels 0.471 meters to the left ( average is 0.417 meters ), and at the end of leg 1 has 1.667 m/s velocity - it also had a momentum change of 5.000 kg.m/s ( 5.000 N.secs ) - it gained translation KE of 4.167 J - BUT had 0.517 J PE GAIN - therefore it had a total Energy gain of 4.684 J - the WD was 4.706 J which is basically consistent with the Work Energy Equivalence Principle ..

N.B. note the system COM icon at the end of leg 1 - it is still centered directly above the middle of the Control cart indicating that the COM for both carts is at the same x-axis position - but it is raised slightly because of the locked swinging pendulum of the swinger raising the GPE ..

When I'm next here leg 2, the reverse leg where we take away the momentum just given ..

...................



...................

[Fletcher]

Here is the second leg ( leg 2 ) where the momentum previously given to the carts is taken away again, so they come to a complete stop washing off their momentum and translational KE gains ..

** the second animation is the full start stop legs 1 and 2 ..

Comments ..

All linear momentum and translational KE gained and then lost again is the same for each leg for both carts ..

Work Done ( WD = fd ) is considered a scalar - when adding both legs together for each cart the WD is the same for each ..

However the swinger pendulums have gained significant GPE by the impulses given to their cart accelerating and then decelerating them causing them to swing upwards in turn gaining PE - this is a surplus of energy ( PE gain <==> 12.4 % ) above what the control cart gained and lost i.e. Total WD equals KE wrt Work Energy Principle ..

ETA .. brief recap - given the same forward and backward impulses - both carts translational KE gained and then lost again is equal when summed to the total WD on them - the swinger has a free bonus of 1.034 Joules of PE gained from the momentum transaction ..

.......

I'll leave you to think about this "free lifting sim experiment" and I'll make and post up a spreadsheet analysis of the legs for discussion in the next day or two .. sim attached ( frictionless best case ) .. n.b.1. ft outputs are the legs accumulated ft to show the total as contrasted to gained and lost mv .. n.b.2 note the system COM double lift as the pends swing upwards and lock etc ..

.........................



.........................



.........................

[Tarsier79]

Work Done ( WD = fd ) is considered a scalar - when adding both legs together for each cart the WD is the same for each ..

Me:

when I measure work done, do I measure the force I put in and the change in the system COM, or do I measure the force I put in, and the specific distance that point moved?

Copilot:

To accurately measure the work done, you need to consider the force applied and the specific distance that point of application moved. Here's the breakdown:

### Key Points:
1. **Work Done (W)**: Work is calculated using the formula:

\[ \text{Work} (W) = \text{Force} (F) \times \text{Distance} (d) \times \cos(\theta) \]

where:
- **Force (F)** is the force applied.
- **Distance (d)** is the distance over which the force is applied.
- **θ** is the angle between the direction of the force and the direction of the movement.

2. **Center of Mass (COM)**: The change in the system's center of mass (COM) is relevant in more complex analyses involving multiple forces and body dynamics, but for calculating work, the displacement of the point of application of the force is what matters directly.

### Practical Application:
- **Constant Force**: If you apply a constant force in the direction of the movement, the work done is simply \( W = F \times d \).
- **Variable Force**: If the force varies along the path, you'd integrate the force over the distance:

\[ W = \int F \, dx \]

### Example:
If you lift a weight straight up, you measure the vertical force you apply and the vertical distance it moves. If you push a block along a flat surface, you measure the horizontal force and the horizontal distance.

### Summary:
To measure the work done, you focus on the force applied and the distance that point moved, taking into account the direction of the force relative to the movement.

Would you like to explore specific examples or dive deeper into related concepts like energy transfer?

Me:

what if I apply force to a cart, and it has bowling balls in it that move, do I measure the distance of the cart, or the distance moved by the cart and the balls?

Copilot:

In this scenario, you'd need to consider both the distance moved by the cart and the movement of the bowling balls within the cart, but they contribute to different aspects of the system's energy and work.

### Work Done on the Cart:
When you apply force to the cart, the work done is calculated based on the distance the cart moves as a whole.

\[ \text{Work on Cart} = F_{\text{applied}} \times d_{\text{cart}} \]

### Movement of Bowling Balls:
The bowling balls moving within the cart change the system's internal energy. If the balls move relative to the cart, you also consider their kinetic energy.

### Total Work and Energy:
1. **Work on Cart**: Focus on the external force applied to the cart and its displacement.
2. **Internal Motion**: The energy due to the internal motion of the bowling balls can be analyzed separately, considering their relative velocity and position changes within the cart.

### Example:
If you push the cart with a force \( F \) over a distance \( d \), the work done by you is \( F \times d \). However, if the bowling balls inside the cart move, you also account for the kinetic energy they gain due to their movement.

### Summary:
For the work done by your applied force, measure the distance the cart moves. For analyzing the total system energy, include the motion of the bowling balls within the cart.

Would you like more detailed examples or calculations related to this scenario?

[Tarsier79]

Me:

if the cart and the bowling balls are moving at 5m/s and I apply a force opposite to its movement, is the FxD relative to ground, or relative to its movement? is the FxD a negative amount because we are decellerating the cart?

Copilot:

if the cart and the bowling balls are moving at 5m/s and I apply a force opposite to its movement, is the FxD relative to ground, or relative to its movement? is the FxD a negative amount because we are decellerating the cart?
When you apply a force opposite to the movement of the cart and bowling balls, here's how you would consider the work done:

Reference Frame:
Relative to the Ground: The force (F) and the distance (D) are typically measured relative to a fixed reference frame, which in this case is the ground.

Work Calculation:
Direction of Force and Movement: Since the force is applied opposite to the direction of movement, it will decelerate the cart. The distance (D) is the displacement of the cart relative to the ground.

Sign of Work:
Negative Work: When force is applied opposite to the direction of movement, the work done is negative because the force is acting to decelerate the cart.

Work (W) = 𝐹 × 𝐷 × cos (𝜃)

where
𝜃 is the angle between the force and the direction of movement. For deceleration:

𝜃 = 180∘
(opposite direction)
cos (180∘) = −1

Work (W) = 𝐹 × 𝐷 × (−1)
Work (W) = − 𝐹 × 𝐷
Summary:
Relative to Ground: Measure force and distance with respect to the ground.

Negative Work: Since you’re decelerating the cart, the work done is negative.

Would you like to dive into more details or other aspects of work and energy?

Me:

So If I accelerate the cart with a given force and it takes a certain distance, then I apply the same force in reverse and it comes to a stop over the same distance, the work done is 0

Copilot:

Correct! If you apply a force to accelerate the cart over a certain distance, and then apply the same force in the opposite direction to decelerate it over the same distance, the total work done over both distances would indeed be zero.

### Breakdown:
1. **Work to Accelerate**:
- \( W_{\text{accelerate}} = F \times d \) (positive work, as force and displacement are in the same direction).

2. **Work to Decelerate**:
- \( W_{\text{decelerate}} = -F \times d \) (negative work, as force and displacement are in opposite directions).

### Total Work:
\[ W_{\text{total}} = W_{\text{accelerate}} + W_{\text{decelerate}} \]
\[ W_{\text{total}} = (F \times d) + (-F \times d) \]
\[ W_{\text{total}} = Fd - Fd \]
\[ W_{\text{total}} = 0 \]

### Summary:
The positive work done to accelerate the cart is exactly canceled out by the negative work done to decelerate it, resulting in a net work of zero over the entire process.

Would you like to explore more examples or dive deeper into related concepts like kinetic energy or energy conservation?

[Tarsier79]

The negative work was a new one to me...

So, in conclusion, the cart with the swingers travels a further distance in phase 1 than the fixed cart, so more work is done. In deceleration, both carts end up at the same position, so less negative work is done on the swinger cart. So in total, you did more work on the cart with the gain in PE in both phase 1 and phase 2 than you did on the cart without. If you correct the calculations, is there still a free lift?