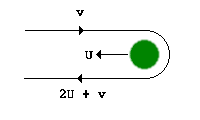
Consider the energy changes as a rider swings around the above path.
The green horizontal legs involve no Newtonian Gravity (NG)change.
Less obviously perhaps neither do the horizontal legs involve any Ersatz Gravity (EG) change since the angular velocity is zero at the beginning and ending of the inner and outer semi-circular legs. Therfore no energy is needed to move the rider in on the right hand side. Neither is any energy given to the rider when he is moved out on the left hand side.
Though the NG energy lost is equal to the NG energy gained for both semicircular legs The range of actual and potential energy covered is greater for the blue leg than the red leg.
Put in another way the rider falls further and rises further in a vertical direction along the blue leg than he does on the red leg.
So the blue NG gravitational span is greater than the red NG gravitational span.
We may view this as a higher order differential for the NG gravity field.
Likewise there is also a higher order differential for the EG field.
In effect the swing mechanism is transducing NG vertical motion into EG rotational motion.
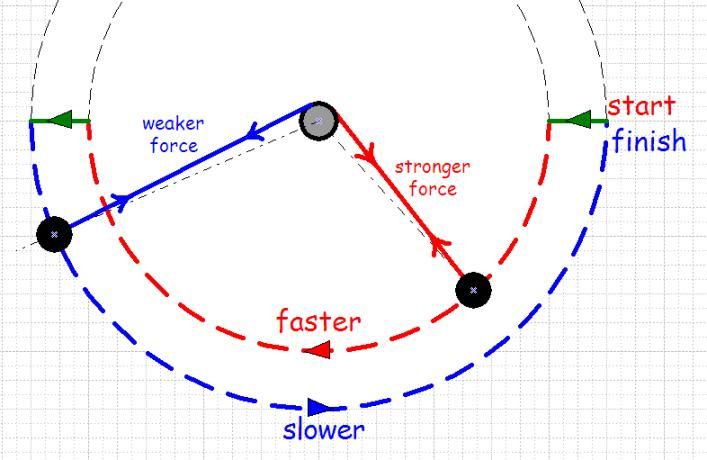
As the rider moves along the red and blue legs he exerts a force on the pivot. This force varies from zero at the left and right zeniths to a maximum at the nadirs.
Because the blue leg is slower, the pendulum being longer and therefore the swing period being greater, the average force exerted on the pivot by the blue leg will be less than the average force exerted on the pivot by the red leg.
If we move the pendulum arms as shown in the above diagram so that they are offset to the centre of rotation then the pivot will be dragged round clockwise by the red arm and counter-clockwise by the blue arm
If the central pivot is braked then more work is done by the red torque, the stronger force, as it swings through +180° than is done by the blue torque, the weaker force as it swings through -180°.
Therefore there is excess clockwise work which drives the central pivot.
So, Differential NG energy is transduced to differential EG energy which leads to rotational energy driving the system clockwise.
The rest is engineering. I was tempted to say merely engineering but I realise these things are never that easy.
It's rather interesting to note that in one of the main drawings Bessler shows a pendulum with an eccentric connection to the main axle.

Was he trying to tell us something?