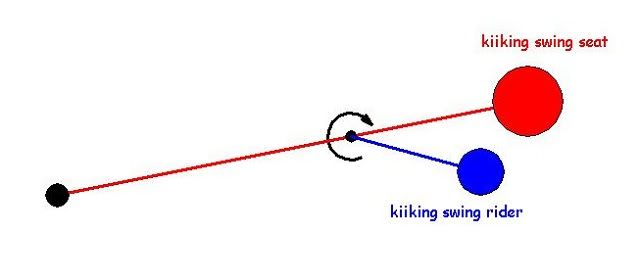
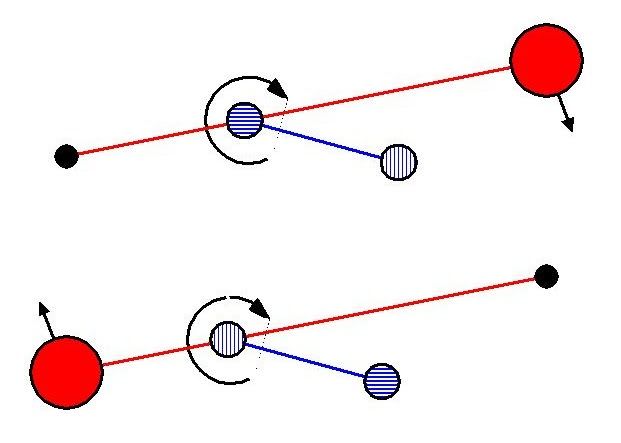
The figure below shows a beam pivoted at the middle with a pair of weights at each end. The leading arm of a pair is pivoted at the centre so that when its weight reaches 2 o'clock, say, it can be released and fall under gravity. It is as though the weight has been transferred to a very low inertia wheel, zero inertia if we neglect the mass of the arm. Thus it is the boundary case of a Keenie Low Inertia Wheel.
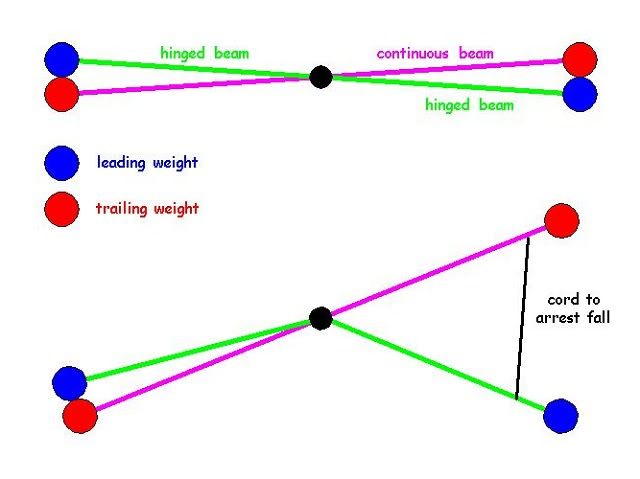
The fall of the hinged half beam is arrested by a cord which transfers the weights kinetic energy to the larger mass of the rest of the beam. Thus we have a situation which is kind of the inverse of Kirk's
"One pound dropped 1 foot launches one 1/4 pound mass 16 feet - their momentum is equivalent.
The ke is 400% dfferent"
except that we are turning KE into rotational momentum rather than the other way around.
Now, it's clear that as far as the vertical gravitational wind is concerned its action is very different on the 12 to 6 side than on the 6 to 12 side.
One could say that on one side KE rules and on the other MOMENTUM rules. We have performed a kind of ju-jitsu on gravity and turned its strength on one side against it on the other.
We can see that the hinged beam resets itself rather conveniently by hanging vertically down until the rest of the beam catches up with it.
The action repeats at 180° with the other hinged half beam and other beams contribute at appropriate angles.
The above argument doesn't pretend to be any proof of anything. It is merely an attempt to set the scene for thinking about how to bias the action of gravity with respect to the two sides of a mechanism.