Morphing Keenie to Bessler

[Grimer]

Good point. I suppose it depends how much of a tug the falling weight gives the rest.

But anyway, the concept has given me the insight to solve the KiiKing problem. In view of your thread on the momentum topic which seems to be well on the way there perhaps I shall call it the Kirk Kiik solution.

And, yes, your suppositions are correct.

More later.

Oops! I seem to have confused you with Kirk, Mark.

You must have wondered what I was on about when I wrote, " In view of your thread on the momentum topic which seems to be well on the way there perhaps I shall call it the Kirk Kiik solution."

Sorry about that.

[Mark]

Not a problem, Frank. I figured that you just forgot to drop the bi-focals from up on your head to down on your nose ;-)
I have a couple of comments about your newer sketches, been too busy today to get on. It's getting late here and need some sleep, will get to it later this morning.

[Grimer]

A problem with the pendulum-Carnot model that has been puzzling me for some time is:
What is the pendulum analogue for pressure? In other words, what is the intermediate stage between Newtonian gravity (NG) potential (temperature) and Ersatz gravity (EG) potential (rotation)?

Current progress has encouraged me to think harder about this. I now realise it's the elastic strain energy in the pendulum arm. This goes from compression at 12 (high pressure) the point of maximum Newtonian potential - minimum Ersatz potential, to tension at 6 (low pressure), the point of maximum ersatz potential and minimum Newtonian potential.

This shows the importance of having both a pendulum arm made of a material with a very high coefficient of restitution and very rigid pivot point if one is to achieve the maximum angle of swing.

Without this below-the-threshold-of-perception exchange between gravity and strain energy pendulums would not swing past the keel point.

It is interesting to note that in the case of the Carnot the gas pressure varies from some positive value to zero whereas in the case of the pendulum it varies from positive to negative. This is because unlike a gas a solid material arm will take tension. Zero "absolute" pressure for a material arm is the point at which it fails in tension.

[Mark]

It's getting late here and need some sleep, will get to it later this morning.

Let's hear it for best laid plans :-/

Switching the pivot ends undoubtedly requires some mechanical ingenuity but it needn't require significant energy.

The switch is dirt simple and takes no energy, really. It's the delayed release of the minor pendulum that gets a little tricky.

Have you considered the effects of CF on the rider deploying correctly ? - snip - better to have it close to the axle.

I agree.

the kick going down and the kick going up would be similar in magnitude

I'm not really sold on the ascending-side kick providing an upward jerk/impulse. I'm thinking that the force would likely be downward on that side, too. Even if it were next to the axle. (I could be wrong)
If it could be applied directly to the axle, then the clockwise force of the jerk would, of course, get transferred and assist the rotation of the major pendulum.

What is the pendulum analogue for pressure? In other words, what is the intermediate stage between Newtonian gravity (NG) potential (temperature) and Ersatz gravity (EG) potential (rotation)?

I don't think there's an intermediate stage, just peaceful coexistence. With a certain amount of give and take.

[Grimer]

Thanks for your thoughtful reply, Mark.

I hope you are wrong about the ascending side kick. Time will tell.

Can't agree with you about the intermediate stage for the reason I gave.

Strain energies are well below the threshold of perception but I'm a bit surprised that you ignore the pressures involved when they are explained.

Also, I can now see that the falling beam jerks correspond to the adiabatic legs of the Carnot.

All will be explained in excruciating detail in due course.

[Grimer]

The half pendulum drops reminded me of this clock from Willy Wonka And The Chocolate Factory.



Let's hope when I open my Wonka Bar there'll be a golden ticket.

[Grimer]

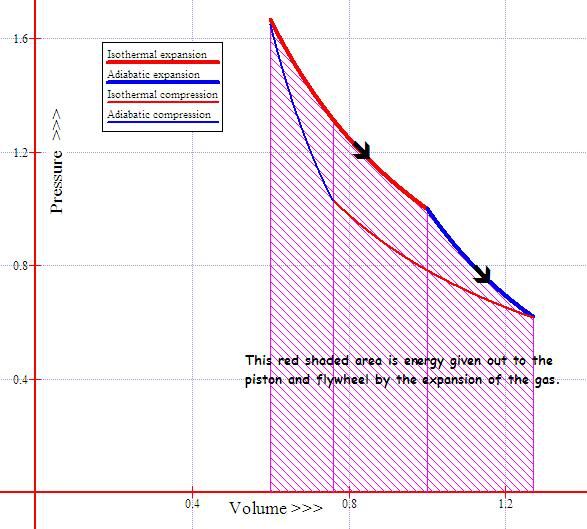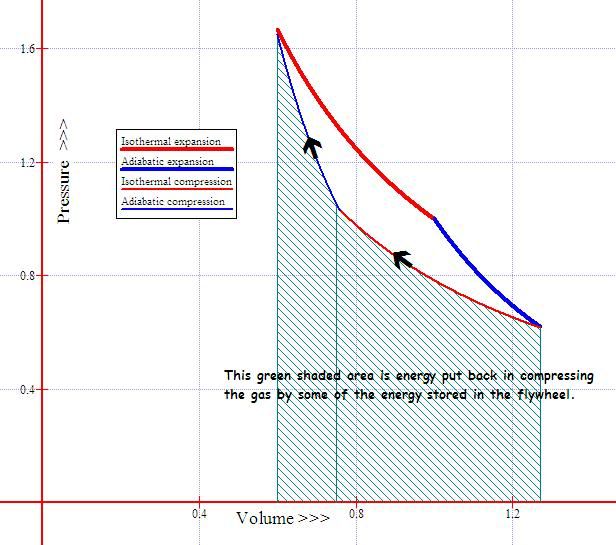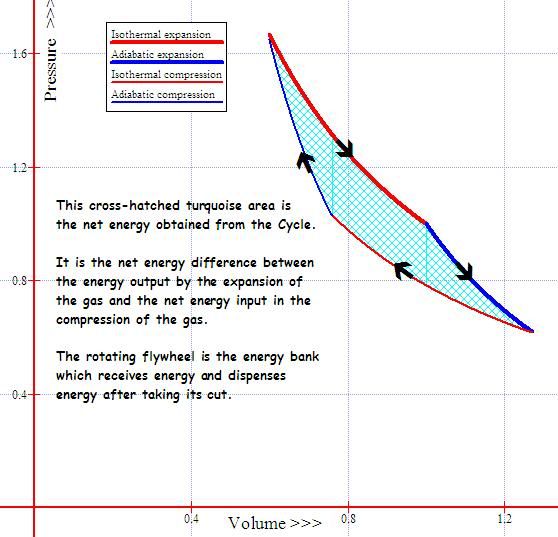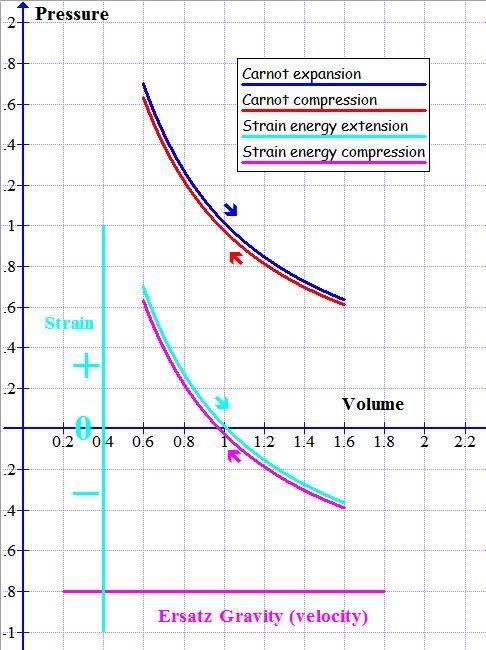
The above diagram shows two sets of pressure volume relations.

The descending and ascending arms have been pulled apart slightly for clarity though, of course, they both lie along the same xy = a constant curve

The top set is the familiar Carnot isothermal expansion and compression.

The bottom set shows the pendulum arm expansion (aka extension) and compression.

The Carnot is shown without the adiabatic legs which means that no
area is enclosed by the cycle and no area is generated. Without any losses the best one could hope for is an eternal oscillation.

Is that perpetual motion of the first kind?

Likewise with the pendulum there is no equivalent to the adiabatic legs and so in the limi all we have is the pendulum rising to its zenith at 12 o'clock and falling to its nadir at 6.

So the problem is to insert the mechanical equivalent of adiabatic legs into the, erm...., let's call it the Bessler cycle.

We can get one helpful clue from the Carnot cycle.

We know that the essential difference between isothermal and adiabatic change in the Carnot is one of speed.

If we change the pressure very slowly in the Carnot then the PV relation will be isothermal. However, if we change it very fast it will be adiabatic because heat won't have time to enter the cylinder and all energy exchange takes place within the cylinder.

Equivalently, of course, is the use of insulation to slow down the transmission of heat. This is the conventional way the Carnot cycle is viewed.

A classic example where speed of change is important is the speed of sound. This even tripped up the sainted Newton. He assumed compressions and rarefactions followed the isothermal equation of

PV = a constant

instead of the correct adiabatic equation of

PV^(5/3) = a constant

and wound up with the wrong answer.

So how does knowing we need something fast to add to something slow help us?

Well, the Keenie shows one way forward. In the Keenie the weight transferred to the low inertia wheel drops faster under gravity than the unbalanced weight on the high inertia wheel.

No doubt members can think of other examples.

[Fletcher]

Grimer .. I won't pretend to understand where you are going with this but assume you can make the connection between Carnot cycles, adiabatic & isothermal processes, Cf's [Ersatz gravity] & Thermodynamics.

In terms of Thermodynamics & mechanical arrangements, IMO, it means a way to introduce heat energy into a system to output useful energy in the form of mechanical work done - CoE still holds true as you are introducing external energy into a system to be converted into mechanical energy to do useful external work i.e. making an open system to the environment.

This would mean that an adiabatic process would be useless to us because it happens so quickly that no heat energy can enter the system from outside the system to do that useful work & it would effectively be a closed system therefore self sustaining & useful external work would contravene CoE & Thermodynamics.

So, it seems to me that the isothermal process is the only one with potential to meet the criteria of a self sustaining mechanical engine which can also output useful external work, be an open system, meet CoE doctrine & be within the bounds of Thermodynamics.

Quite how Cf's, strain & compression, Carnot cycles & fast & slow rise & fall can achieve this mechanically without introducing heat energy into the equation is way beyond my current understanding.

In fact, IMO, strain, compression, collisions & physical exchanges etc create heat which reduces the useful mechanical potential whereas I would think we want to create an adiabatic cold sink, from mechanical processes, that can then warm slowly [isothermally] thus introducing external heat energy, forming an open energy system !

I look forward to your logic & a convincing argument to show otherwise.

I posted here on your thread because often you are a lone voice in the wilderness yet people do read even if they don't follow.

[Grimer]

Thank you for your post, Fletcher. I'll have to think about it for some time in order to frame you a useful answer.

[Richard]

Grimer...thanx much..

no rush for this...but, when possible..

..for the carnot process (engine) what is our ( Gas) ...The Isentropic properties of expansion...? PV constant

Is your Idea...to employ system heat generated...through "scroll compression" and if so...is water going to cold sink ( condense) the gas?

summary

can we draw parallels between your work and Path_finders recent post of "Fermadd" closed nitrogen system.

richard.

ps. I know you've worked with this much longer than any recent mention of "Fermadd"..it is referenced only to help (Me) understand..:-)

[Fletcher]

I think Grimer just draws the analogy to the Carnot cycle, adiabatic & isothermal processes, in relation to the inertial properties of the slow & fast moving sections of the wheel.

The point I'm making with him is that they are NOT analogies but the likely actual physical processes that are most probably necessary to result in FE/OU/PM via mechanical means - therefore the inertial qualities & stress & strain are analogies of the Carnot cycle & adiabatic & isothermal processes, & not the other way around IMO.

That is if you adhere to CoE & Thermodynamics - if you don't then you're cutting your own track thru the bush ;7)

Or I could have completely misunderstood him which I'm sure he will clarify.

[Richard]

thanx Fletcher..this may be my confusion..

Grimer states...from // General Topics // the Bessler Jigsaw //

""And that has given me a great idea. I think I may be able to show that the jerk energy solution is a heavily disguised conservation of angular momentum. Also, two different rotations suggest that one is a power cycle, the other is a refrigeration cycle with three revolutions as isothermals without the adiabatic legs ""

My assumption...is a literal one based on above statement..

If this is the case...Pressure / Volume and adiabatic and isothermal processes would include a gas.

think maybe Grimer is holding out on us a little../ :-))

[Grimer]

Grimer .. I won't pretend to understand where you are going with this but assume you can make the connection between Carnot cycles, adiabatic & isothermal processes, Cf's [Ersatz gravity] & Thermodynamics.

In terms of Thermodynamics & mechanical arrangements, IMO, it means a way to introduce heat energy into a system to output useful energy in the form of mechanical work done - CoE still holds true as you are introducing external energy into a system to be converted into mechanical energy to do useful external work i.e. making an open system to the environment.

This would mean that an adiabatic process would be useless to us because it happens so quickly that no heat energy can enter the system from outside the system to do that useful work & it would effectively be a closed system therefore self sustaining & useful external work would contravene CoE & Thermodynamics.

So, it seems to me that the isothermal process is the only one with potential to meet the criteria of a self sustaining mechanical engine which can also output useful external work, be an open system, meet CoE doctrine & be within the bounds of Thermodynamics.

Quite how Cf's, strain & compression, Carnot cycles & fast & slow rise & fall can achieve this mechanically without introducing heat energy into the equation is way beyond my current understanding.

In fact, IMO, strain, compression, collisions & physical exchanges etc create heat which reduces the useful mechanical potential whereas I would think we want to create an adiabatic cold sink, from mechanical processes, that can then warm slowly [isothermally] thus introducing external heat energy, forming an open energy system !

I look forward to your logic & a convincing argument to show otherwise.

I posted here on your thread because often you are a lone voice in the wilderness yet people do read even if they don't follow.

It's nothing to do with heat. The Carnot cycle is being used as an example of the transfer of rotational (closed path) motion from one scale to the next. In the case of the Carnot it is from the rotation of atoms via the variable pressure (which can also be viewed as closed path motion) to ultimately the rotation of the flywheel.

Changing the way the levels are connected leads to a change in the direction of energy flow.

This can be illustrated by a familiar example.

If you whirl around a weight on the end of a string and keep it at a constant angular velocity then energy is flowing from your hand to the stone via the string (analogous to the Carnot refrigeration cycle). The string is making a slight angle increase to the radius which is pulling the stone around against the resistance of air pressure. Were it not for air resistance the stone would be accelerating.

Now if you let the stone decelerate then it will start pulling your hand around and energy will be flowing from the stone to your hand (analogous the the Carnot power cycle).

As far as the Carnot cycle is concerned you need both the isothermal legs and the adiabatic legs to enclose an energy area. The energy obtained is a function of the area enclosed. So one needs to understand what it is in the combinations of variables which give you the same functional relationships as the Carnot cycle.

Clearly, strain in the components of the wheel is analogous to pressure which is one approach. But probably seeing acceleration and jerk as the analogues of isothermal and adiabatic is more promising.

[Richard]

the butterfly effect??

...clearly out of my league Grimer...I shall follow, listen...and maybe learn...

richard

[Grimer]

I have copied the following post from something I wrote on the Grimer forum some time ago. I hope this helps.


============================================
By thinking about the Carnot Cycle (CC) I have come up with a new way of looking at the problem of obtaining energy from gravity.

As I've said before the CC consists of three very different scale of rotation. The atoms (Compreture = 1/temperature, i.e. the reciprocal of temperature), the closed path translation of those atoms (Pressure) and the rotation of the flywheel driven by the piston (volume).

Now if you look a the CC diagram


1
This red shaded area is energy given out to the
piston and flywheel by the expansion of the gas.



This green shaded area is energy put back in compressing the gas by some
of the energy stored in the flywheel.



This cross-hatched turquoise area is the net energy obtained from the Cycle.

It is the net energy difference between the energy output by the expansion of the gas and the net energy input in the compression of the gas.

In short, the energy gained in the cycle is the relatively small difference between the energy put out and the energy put in. It is analogous to the traders difference between his buying price and his selling price. It is the Carnot Cycle's PROFIT.

The rotating flywheel is the energy bank which receives energy and dispenses energy after taking its cut.

This situation is analogous to the action of a child on a swing (a parametric pendulum or oscillator). A small amount of energy is put in each arc that the swing makes. This demands co-ordination on the part of the child. Initially this is difficult for children to master, as is the riding of a bike. But with persistence they eventually get it - and so will we.