Big Troubles Brewing For The Theoretical Physics Smart-Set!!!

[daxwc]

I think that's a great idea Dax. Frank has no animosity towards you because his religion trains him to not react that way. Isn't that admirable? Frank's a great guy really.

Maybe; religion or a form of trolling? Religion doesn’t stop you from expressing an opinion or protecting yourself within a limited measure. I also didn’t mean to hurt yours or Grimers feelings with my boorish comments, but if 15 people tell you to change you would think that it would register.

So we can play a game if you like. For each time you slam Frank, I slam you harder. Isn't that a nice game? I think so.

You mistake me for someone who gives a shit 8)…

OK Dax I started writing a response to your questions but then I realized I would be giving tacit approval to your abrasive and boorish behavior on the forum.

And you still did 8)

[primemignonite]

Gentlemen,

Please!

No circular firing squads here.

The real enemy is not us; we are not of that snide Smart-Set of growing infamy.

It was all going so well with a final, provisional resolution seeming within grasp.

Please, let's not descend into base rancor, OK?

All the Best(s)!

James

[Grimer]

Another example of an asymmetric force moving the earth is the very familiar case of a body rolling or sliding down a slope.



The diagram above shows the normal and reaction forces of a body on a frictionless slope. The red arrow shows the horizontal force acting on the slope. This horizontal force pushes the slope to the left.



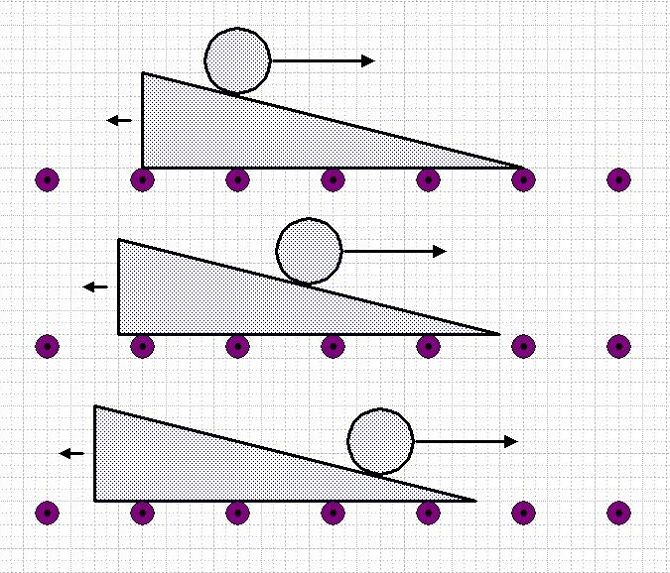
The effect of this push can be seen by mounting the slope on rollers as above. The relative accelerations of the body and the slope will be in inverse ratio to their masses.

In this case the mass of the slope is substantially greater than the mass of the body so the acceleration of the body will be substantially greater than the acceleration of the slope.

Consequently, the movement of the body to the right will be greater than the movement of the slope to the left as shown in the three diagrams.



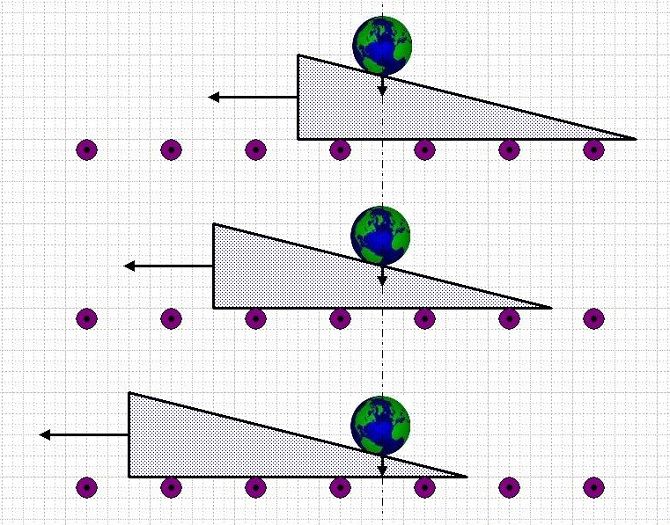
Next consider the boundary case where the mass of the body is vastly greater than the mass of the slope. In this instance the mass will fall almost vertically (but not quite) and spit the slope out to the left.

(Which reminds me of the time during the war when we were given prunes and custard for school dinner's pudding. We used to squeeze the slippery prune stones between our fingers and fire them down the hall.)

The opposite boundary case is where we remove the rollers and attach the slope to the earth. Now the slope and earth will accelerate to the left. The acceleration will be well below the threshold of perception but it will not be zero.

[cloud camper]

All right Frank, wrt your previous post, I am with you.

I hope you're considering the response time in this scenario. That is, we get an instantaneous and one time static response that statically balances the outer wheel against the ratchet.

But the dynamic response of the earth to this imbalance (torque couple) could take thousands of years to produce the most incredibly small displacement and could not be measured with the most sensitive equipment imaginable and by then our tower would have disintegrated into dust!

Yes in theory, the earth would be displaced but practically speaking one would say this effect is "vanishingly small" and occur over such a huge time period no one would be around to measure it!

[Grimer]

We do not get a static response, we get a dynamic response - else we break the conservation of angular momentum law. Statics is always dynamics if you look closely enough.

A still picture on a TV screen may look static but it isn't.

What happens to the earth is irrelevant. We are only concerned with the removal of angular momentum to the earth, not what happens to it.

I've no doubt that when Newton talked about a gun that could fire a cannon ball horizontally so fast that it would fall continuously towards the earth people complained that there was no gun capable of that feat.

The art of reasoning consists in getting hold of the
subject at the right end, of seizing the few general
ideas that illuminate the whole, and of persistently
organizing all subsidiary facts around them. Nobody
can be a good reasoner unless he has realized the
importance of getting hold of the big ideas and
hanging onto them like grim death .

A.N.Whitehead

Presidential Address to the London Branch of the
Mathematical Association., 1914

[cloud camper]

Yes Frank, the dynamic response would begin immediately, but it would take
thousands of years to complete and then would still be unmeasureable.

This would be like throwing a banana on one side of a seesaw that was previously balanced with lets say an identical aircraft carrier on each side.

Yes in theory there would be a dynamic response (ignoring friction) but the dynamic response time before any actual measureable displacement would occur would be on the order of decades due to the stupendous inertia to be overcome. What am I missing?

[Grimer]

Is anybody else having Cloud Camper's problem?

Although perhaps in view of the obvious cognitive dissonance involved I should ask.

Is anyone not having Cloud Camper's problem?

[cloud camper]

Yes, I agree this removal of angular momentum to the earth would occur and begins immediately but what I see is that it would take thousands of years to complete equalization.

When the earth finally completed this equalization, only then would we have conservation of angular momentum. In the meantime, the earth would be subjected to a continual (but decreasing) almost infinitely small torque that would cause it to accelerate to it's eventual angular velocity that would produce an eventual conservation of angular momentum.

The earth, due to it's immense inertia, cannot adjust it's angular momentum instantly and it becomes a lengthy process.

The smaller the imbalance, the longer the dynamic response time until equalization.

Here is an example. We have an electric motor driving a 100 lb flywheel through a axial coil spring at 1000 rpm. Everything is stabilized.

Now almost instantly we double the rpm of the motor. What happens? The flywheel is still spinning at 1000 rpm and cannot adjust it's rpm as quickly as the motor. The motor end of the spring is now turning 2000 rpm, the flywheel end is still at 1000.

So all this new energy goes into winding up the spring. The spring then begins releasing this energy into the flywheel but it doesn't occur instantly.
Then after a time the flywheel accelerates to 2000 rpm. Only then is angular momentum equalized. Until then there is a continual but decreasing spring torque on the flywheel that acts to accelerate it to match the motor rpm. When the flywheel has finally achieved 2000 rpm, the spring torque decreases to zero and rpm equalizes.

Now lets repeat the experiment but instead of doubling the motor rpm we only increase it by one rpm. What happens? The new energy goes into the spring but the imbalance is so little, the flywheel barely notices it. The flywheel is in no rush to compensate. After a while, the flywheel says OK, I will speed up a little but what's the rush? I'll just take my time, thanks. So eventually, we achieve equalization but it will take much longer than before.

That's what I see Frank, maybe I'm wrong!

[Grimer]

Once counter clockwise action has left the large wheel it doesn't matter a fig what happens to it. We are not interested. The fact is it has left and its not coming back.

However, it's clear that you are hung up on this so we'll just bypass it for now and proceed with the next part of the argument.

I'll have to draw up some diagrams.

[daxwc]

Doc’s “Heathen� has been analysed and physically built by others, such as Ralph and I don’t think they got it wrong. All have claimed the wheel will not run as configured and missing a major component at the very least. Maybe the forum can focus on what is missing?

The fact that it was called the Heathen probably gives some indication if it ever really worked.

I'll have to draw up some diagrams.

You might not need to; just refer members to your Blog.

[rlortie]

Doc named the machine designed by Albert Keno and forged by third parties in 1909 "The Heathen" because of its weight and the fact that the 12.5 weights raised hell pinching fingers.

To my knowledge the machine was nameless by all until Doc referred to saw blades in describing its depiction. The term BuzzSaw was thus born here on this forum. To Doc it was always the "The Heathen"

Ralph

[cloud camper]

Doc’s “Heathen� has been analysed and physically built by others, such as Ralph and I don’t think they got it wrong. All have claimed the wheel will not run as configured and missing a major component at the very least. Maybe the forum can focus on what is missing?

"Absence of evidence is not evidence of absence."

Carl Sagan invoking cosmologist Martin Rees.

[Grimer]

@ cloud camper

I think I see a way of viewing things which you might find acceptable.

Consider the first case of no one one way clutch.

Gravity pushes down on the 3 o'ck weight giving it 5 units of CW angular momentum, say.

Gravity also pushes down on the 9 o'ck weight which takes the other weights with it giving the total 5 weights 5 units of CCW angular momentum. The sum of the two angular momentums is zero as it should be since for an rotationally isolated system angular momentum must be conserved.

Now consider the second case of the one way clutch in operation.

As before, gravity pushes down on the 3 o'ck weight giving it 5 units of CW angular momentum.

But when it comes to the 9 o'ck weight it finds it can't push it down at all because the one way clutch at the tower is keeping the 9 o'ck weight stationary.
The 9 o'ck weight makes no CCW (or CW) angular momentum contribution to the two wheel system.

So now the two wheel system has just the 5 units of 3 o'ck weight CW angular momentum.

At present this angular momentum is carried by the 3 o'ck weight but when that weight interacts with the other weights the angular momentum will be redistributed in a way which I will go into when the present stumbling block has been removed.

[daxwc]

Cloud:

"Absence of evidence is not evidence of absence."

Actually there are witnesses to say there is missing sections; which is better than your Bessler witnesses, because they actually got to see the mechanism of movement, but are lacking the more critical evidence of perpetual motion. That and reconstructed models do not run, so something is absent.

Ralph:

My research and accumulation of data gathered from family members pretty well confirms that the jack or lay shaft with related sprockets were missing. Also the wood frame work that the unit was supported by was burned for firewood.

The jack or lay shaft, bearings and any other metal related pieces were collected by a scrap iron dealer. Story has it that the only reason the main wheel unit, shaft with one connected sprocket and weights were left behind is that they were rusted together and the collector could not lift it into his truck.

I didn’t know that Ralph; I thought Albert named it.

[cloud camper]

@ cloud camper

I think I see a way of viewing things which you might find acceptable.

Consider the first case of no one one way clutch.

Gravity pushes down on the 3 o'ck weight giving it 5 units of CW angular momentum, say.

Gravity also pushes down on the 9 o'ck weight which takes the other weights with it giving the total 5 weights 5 units of CCW angular momentum. The sum of the two angular momentums is zero as it should be since for an rotationally isolated system angular momentum must be conserved.

Now consider the second case of the one way clutch in operation.

As before, gravity pushes down on the 3 o'ck weight giving it 5 units of CW angular momentum.

But when it comes to the 9 o'ck weight it finds it can't push it down at all because the one way clutch at the tower is keeping the 9 o'ck weight stationary.
The 9 o'ck weight makes no CCW (or CW) angular momentum contribution to the two wheel system.

So now the two wheel system has just the 5 units of 3 o'ck weight CW angular momentum.

At present this angular momentum is carried by the 3 o'ck weight but when that weight interacts with the other weights the angular momentum will be redistributed in a way which I will go into when the present stumbling block has been removed.

OK Frank, that's simple enough. I buy it!

Let's just leave the Earth out of it. For all practical purposes, it doesn't
move or accept angular momentum.

If an asteroid hit the Earth at an oblique angle, then we can talk about it!