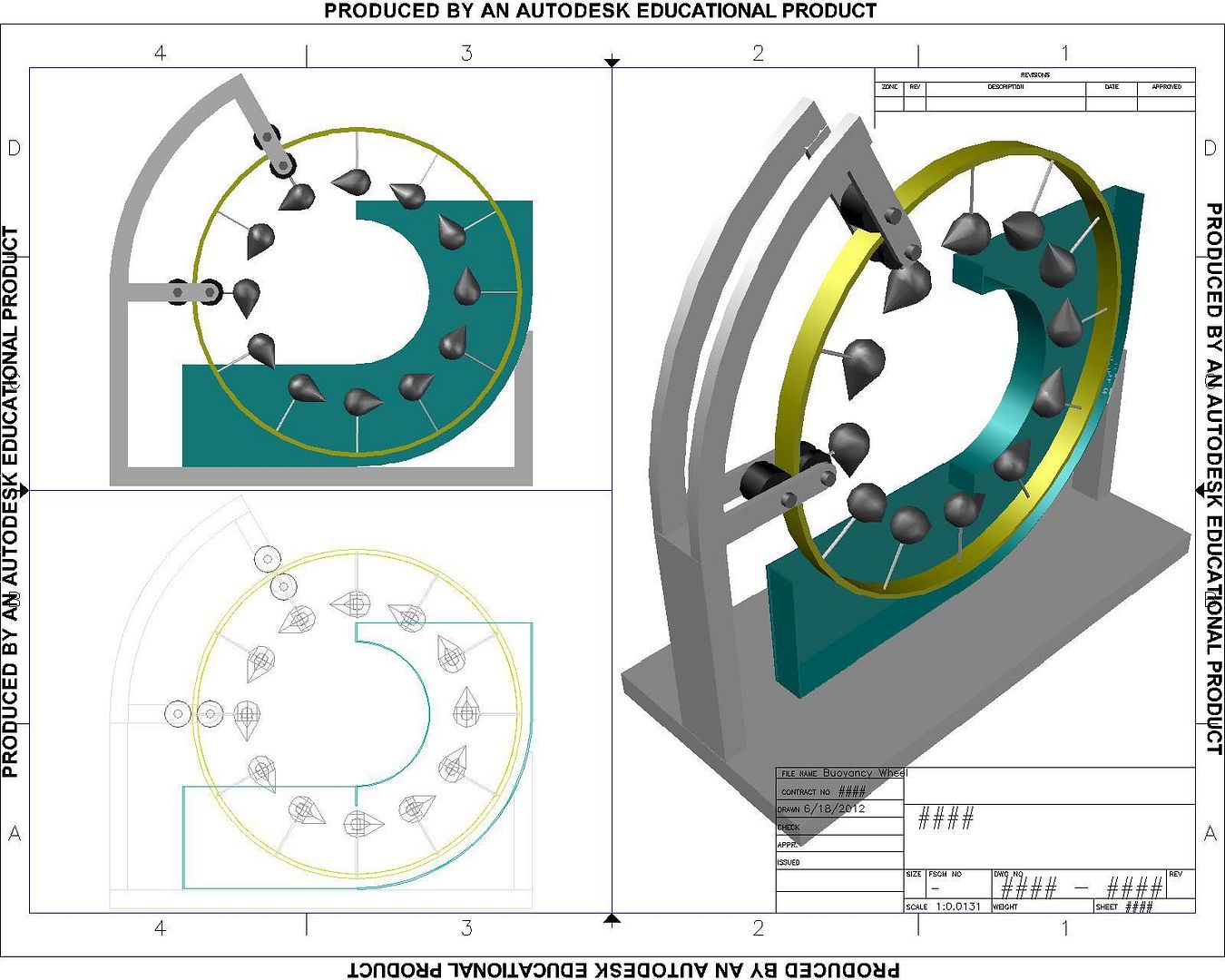
Buoyancy Wheel Design

[Silvertiger]

Drew it this morning. Fill er up. :)

[getterdone]

Hi Sivertiger, this one has been discussed here before, and there are a few patents regarding this type of design that are interesting. The devil is in the details, one that I liked was using air pressure to keep the wet and dry sides seperatrd.

If you do some reserch on this site, I'm sure you'll find plenty of food for thought

[getterdone]

Here's the one I was thinking of, it's from Jim's website

http://my.voyager.net/~jrrandall/McCoinPatent.html

[Silvertiger]

I considered the fact that you need either a pressure differential or something in it's place, and I did come up with a solution for the latter: oil. Add oil to mix and you've solved your problem. Oil is lighter than water, but still has plenty enough mass and density to suit my purpose. Ever seen something form a novelty shop that has a ship floating on water, but is submerged under a less dense fluid? Anyways, that's my idea for it - the most economic, cost-effective, and certainly the most efficient one that I could think of that I know would work.

[Silvertiger]

The oil is the the yellow fluid on the top left and the rest is water.

[Silvertiger]

Of course I'm foreseeing that during the cycle, some oil may cling to the weights and get distributed to the top of water on the other side of the tank. I wonder how much over how much time though. Hmmm... Anyway the purpose of the oil is to bypass the need for Mr. Pascal, hee hee. :)

[Silvertiger]

By the way, it's difficult to see the bisecting piece in the middle of the tank that separates the tank into two halves.

[Silvertiger]

Went to Wallyworld...first test complete; Pascal holds true to his word. I made this tiny tank from a "Stackable Storage" item from Walmart,
added some food coloring to water, and filled the tank half way. Then I added oil to the left side. The results are great. The divider in the middle has a quarter inch gap at the bottom; osmosis did the rest, and the oil raised the water level on the other side.

Top View:


Side View:


Perspective View:

[Tarsier79]

Great work on the experiment! It truly is a beautiful thing!

What you will find, is the different in density of the liquid will be made up by the additional height of fluid on the left hand side. IE an object will be more buoyant on the right, the fluid will exert a certain force over a distance, but on the left, the force will be less, but the distance will be more. Unfortunately for your design, it will show a mathematical equilibrium, once again showing the conservation of gravitational force.

[Silvertiger]

The buoyant force directly opposes the force of gravity in direction. It's magnitude depends,
of course, on both the volume and the density of the mass that displaces the water.
The goal is to create an imbalance of forces using those available to use. Of course
gravity is uniform throughout...that's what this whole dance is all about. lol :)

To create this imbalance using buoyant forces, I used water and olive oil. the density of the oil
is about 800kg/m^3 and for water it is 1000kg/m^3. All I have to do now is manufacture an
aerodynamic weight with a density of 900kg/m^3. According to physics, it WILL sink in the oil.
With many of these on a wheel, it should have enough angular momentum to clear the few
inches of water at the base, pass under the divider, and rise on the side filled with water.

[jim_mich]

I used water and olive oil. the density of the oil is about 800kg/m^3 and for water it is 1000kg/m^3.

Let's do the math!
(I'll use undefined generic units of measurement.)

Conditions:
Density of oil = 0.8
Density of h2o = 1.0
Density of orb = 0.9

Height of oil = 5 units above the oil & h2o interface zone.
Height of h2o = 4 units above the oil & h2o interface zone.
Height of air = 1 units from h2o level to oil level.

5 height units of oil at 0.8 density = 4 units of oil weight.
4 height units of h2o at 1.0 density = 4 units of h2o weight.
Thus h2o at 4 units high balances oil at 5 units high.

The orb will sink in oil and rise in h2o.

The orb in oil produces -0.1 units of downward force. (It sinks on left side.)
The orb in h2o produces +0.1 units of upward force. (It floats on right side.)

So, in operation...
The orb sinks in the oil with a force of -0.1 for a drop distance of 5 units.
This produces 0.1 × 5 = 0.5 units/distance of work force. (CCW travel force per picture)

The orb floats in the h2o with a force of +0.1 for a height distance of 4 units.
This produces 0.1 × 4 = 0.4 units/distance of work force. (CCW travel force per picture)

The orb is either lifted or it falls through the 1 unit height of air.
The force is 0.9 × 1 = 0.9 units/distance of work. (CW travel force per picture)

It is assumed the motion thru the air at the top, (up, over, and down) is balanced either side.
It is assumed the motion thru the h2o at the bottom, (down, over, and up) is balanced either side.

So, in summary...
We get 0.5 units/distance of CCW work force as the orb sinks in the oil.
We get 0.4 units/distance of CCW work force as the orb rises in the h2o.
We get 0.9 units/distance of CW work force as the orb rises in the air.

So 0.5 CCW force + 0.4 CCW force equals against the 0.9 CW force.
The dang thing balances.

I have done these type of calculation hundreds of times, and it still amazes me each time when things balance out. But I still have fun doing them when time permits.


Hopefully I've not made any typing or math errors .

[Silvertiger]

Errors:
1. Density is not weight; its is the mass per unit volume of a substance. You multiplied a height of 5 by a density of 0.8g/cm^3,
but let's call it 800 since I prefer to work with kg/m^3.
Was the height you used 5cm, 5m, 5in...? Nevermind...let's call it 5m to keep units the same.

(5m)(800kg/m^3)=4000kg/m^2

What you have effectively done here is defined BMI for some reason, a calculation primarily used in sports and medicine.
Whomever this represents is clearly the most obese creature in the world.

Until this is addressed, I won't even attempt a guess at anything else. :)

P.S.
Weight is measured in SI units as N/s^2, which is kg*m/s^2; in English units it is ft*lb/s^2

Density is measured in SI units as kg/m^3; in English units it is lb/ft^3

Exercise: Negating rotational motion, calculate the resultant force of the linear forces at play (weight and buoyancy)
of a mass of 5kg with a density of 900kg/m^3 in water (density 1000kg/m^3). Then do the same thing for the same mass in oil, density 800.
Subtract the solutions to find the difference. Then imagine that both masses are on a pulley, and figure out which one will rise and which one will not.

[jim_mich]

You can use any desired units. Just plug in the values. The results will be the same.

My mind normally 'thinks' in specific gravity. Water = 1. Your oil (according to the info you posted) has a specific gravity of 0.8. Thus its density is 0.8 relative to water.

My mind 'visualizes' weights as pounds and ounces. This is because I have used these English measurements for over 60 years. I have an old scientific pocket calculator (HP48 sx) that is able to convert most any unit to most any other unit. I can give you mass weight as kilograms, grams, pounds, US ounces, slugs, lbs troy, tons, UK tons, oz troy, carats, grains. I can give you lengths as meters, centimeters, millimeters, yards, feet, inches, light years, kilometers, miles, US miles, chains, rods, fathoms, US feet, mills, microns, and few others even.

My point is that the units used are not relevant. And since this is a world wide forum, most of the time I uses generic units without the need to limit it to any specific system of weights and measures. The calculations are universal. Just plug in your values from your system of weights and measures.

Exercise: Negating rotational motion, calculate the resultant force of the linear forces at play (weight and buoyancy)
of a mass of 5kg with a density of 900kg/m^3 in water (density 1000kg/m^3). Then do the same thing for the same mass in oil, density 800.
Subtract the solutions to find the difference. Then imagine that both masses are on a pulley, and figure out which one will rise and which one will not.

This is exactly what I did! The point that you missed was that your buoy needs to rise from the top of the water up to the top of the oil level, and that rise negates the torque produced by the buoy in the liquid. Any rise of the buoy up to the pulley, around the pulley, and back down to the liquid will balance on both sides. The same happens at the bottom. But you cannot negate the rise of the buoy from the top of the water to the top of the oil. That rise distance times the weight of the buoy will negate the unbalance of the buoy in the oil and water. The system will balance.

This may be the last time I attempt to help anyone. I never know whether to give complex examples that go over peoples mental capacity, or to give very simple examples that leave out all the irrelevant bothersome details. I can do either. But I find it insulting when people tell me I'm wrong. True, I'm only human and do make mistakes, but to lecture me on basic concepts like mass density and such is just plain insulting.

[Bill_Mothershead]

I have never been much into buoyancy but this thread is great.

OK...sink in oil but float in H20...got it!

How about changing the shape of your oil "container"
into a funnel pointing down.

AND...instead of talking about a single floatable item
try to imagine thousands of small beads sinking,
constrained by the shape of the funnel, pushing down
on the lowest bead.

This changes the density equations considerably since
now you have to account for the weight of the beads
pushing down.

Likewise, you could have, in the H20, a funnel pointing up,
to capture the floating-up beads. The goal being that
they just might push a few beads above the surface and
thus be directed to "spill over" into where the oil begins.

Additional note: I have in my house somewhere a child's toy
with two non-mixable liquids. A red-colored liquid forms
small blobs that run a maze as they sink to the bottom of
the toy. (The other liquid is clear and I always assumed it
was just H20.) The child inverts the toy to get the red
fluid to run the maze in reverse.

I don't know the chemistry of the red fluid...but my point is
that there is more than just oil and water. I am almost
certain there are several/(many?) fluids that do not
mix with each other and you could have at least 3
layers of these things in one container.

[jim_mich]

Yes, this would be a really great concept, if only it would work. Unfortunately it will never work as imagined.

In the attached drawing pink oil floats on top of the blue water. The yellow beads are heavier than the pink oil on the left side and lighter than the blue water on the right side and at the bottom. Thus the beads sink in the pink oil and rise in the blue water.

At the top, the yellow beads move sideways though the air and thus both sides are balanced. Likewise at the bottom the beads move sideways through the water and again both sides are balanced.

One might think that this arrangement might produce perpetual motion of the beads. The reason it will not work is because the yellow beads must move though the air for a short distance above the water on the right side. This air travel distance will exactly equal a height that is relative to the ratio of the densities (specific gravities) of the oil and water columns. This travel distance with the beads exerting their full weight force will exactly cancel out all the buoyancy force

Regardless of the densities of the fluids and beads or the dimension used, the buoyancy on the left always equals the buoyancy on the right.