This evening i modelled the revision i mentioned in my last post of that thread - now kiiking by controlled application of counter-torques from accelerating then decelerating an angular inertia, rather than by applying the ice-skater effect; the result is the same, of decelerating the drop phase whist accelerating the lifting phase relative to gravity's constant acceleration, thus garnering a consistent per-cycle momentum gain from gravity and time, but no longer reliant on an input workload that squares with RPM as CF-PE does, instead the only workload now being accelerating and decelerating angular inertia.
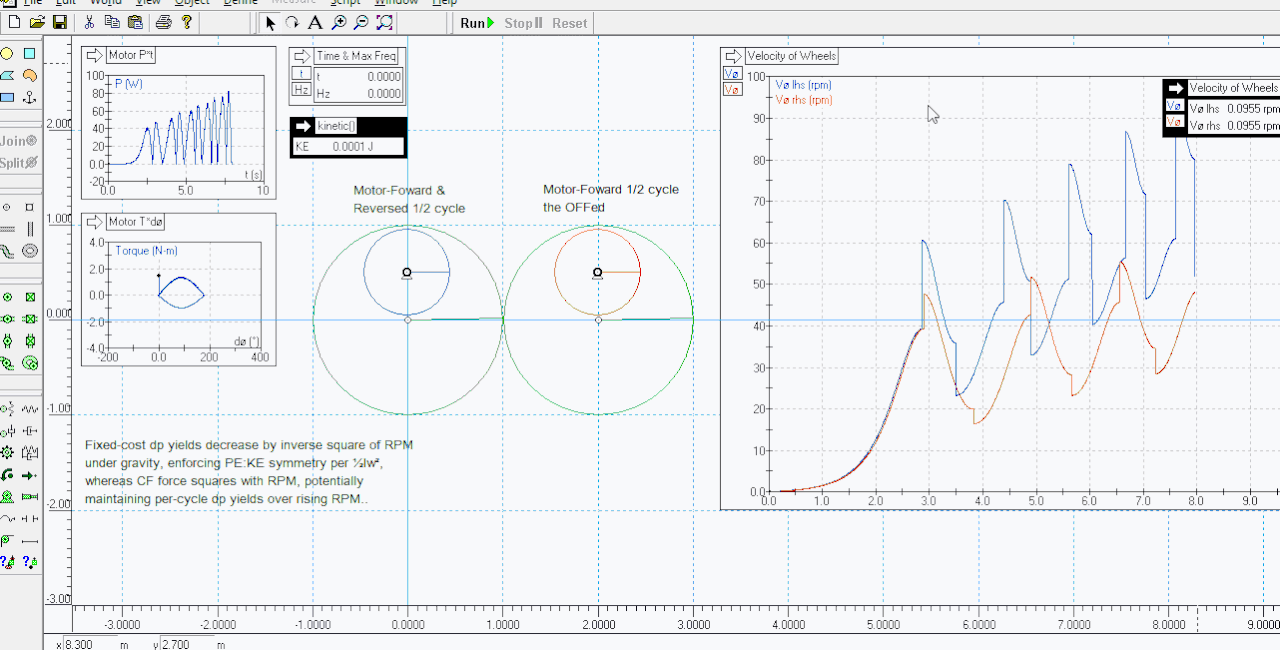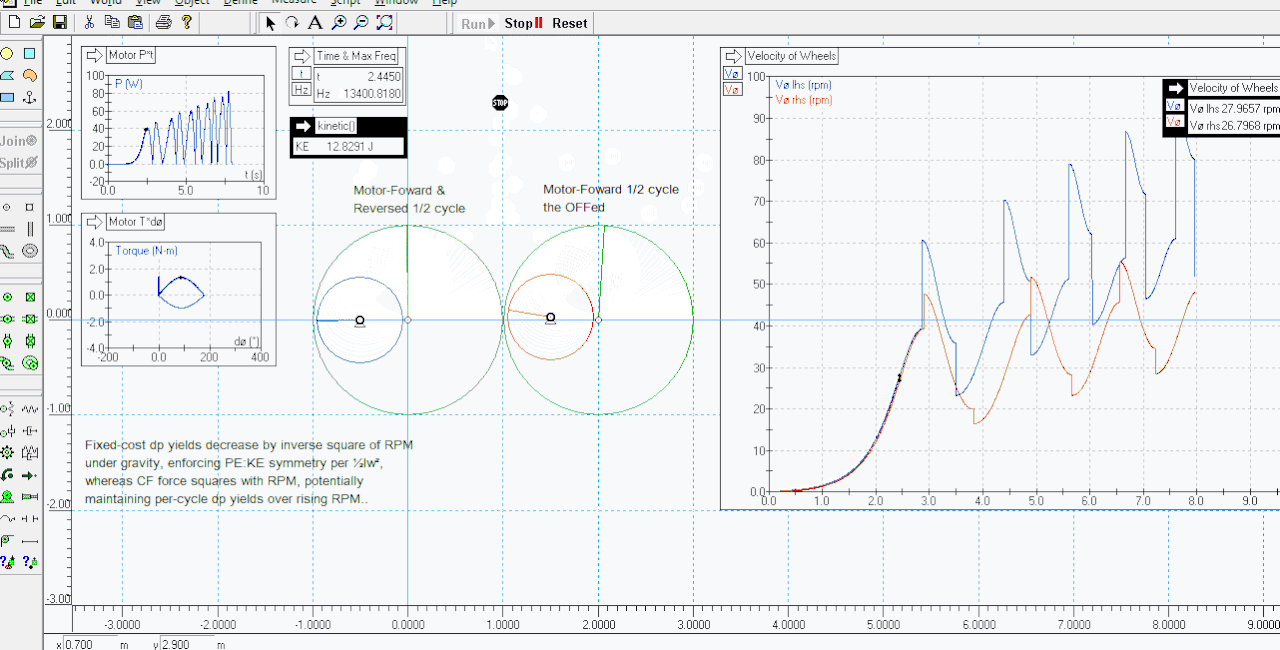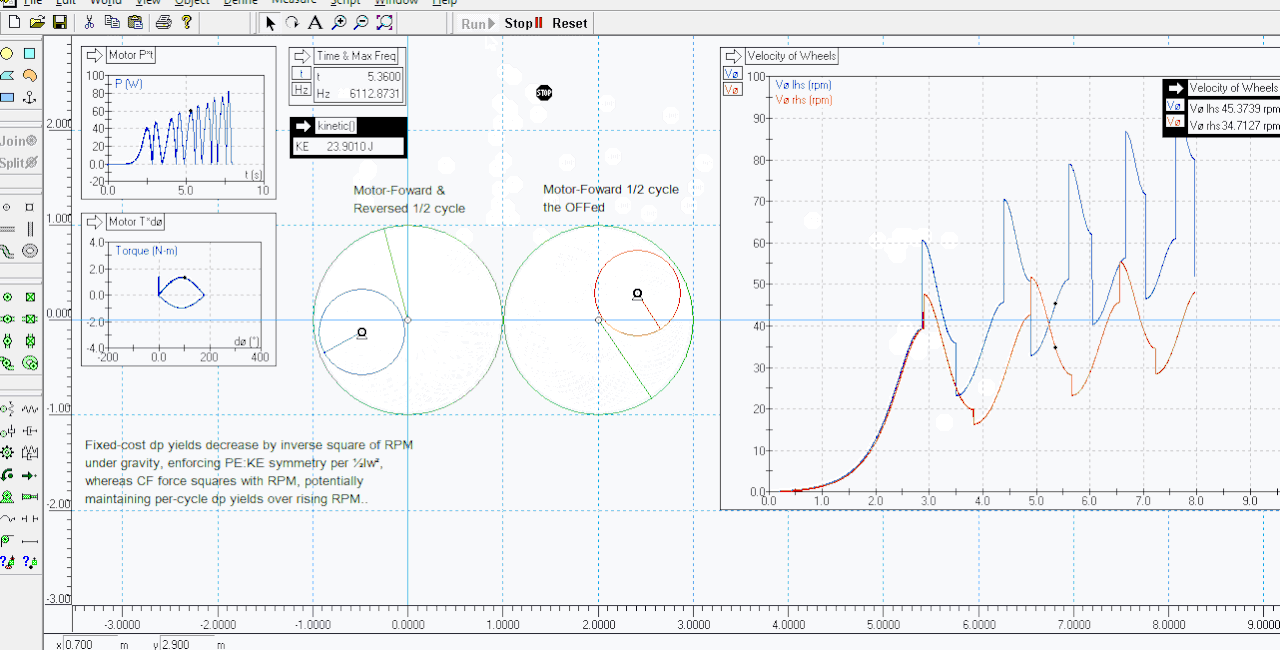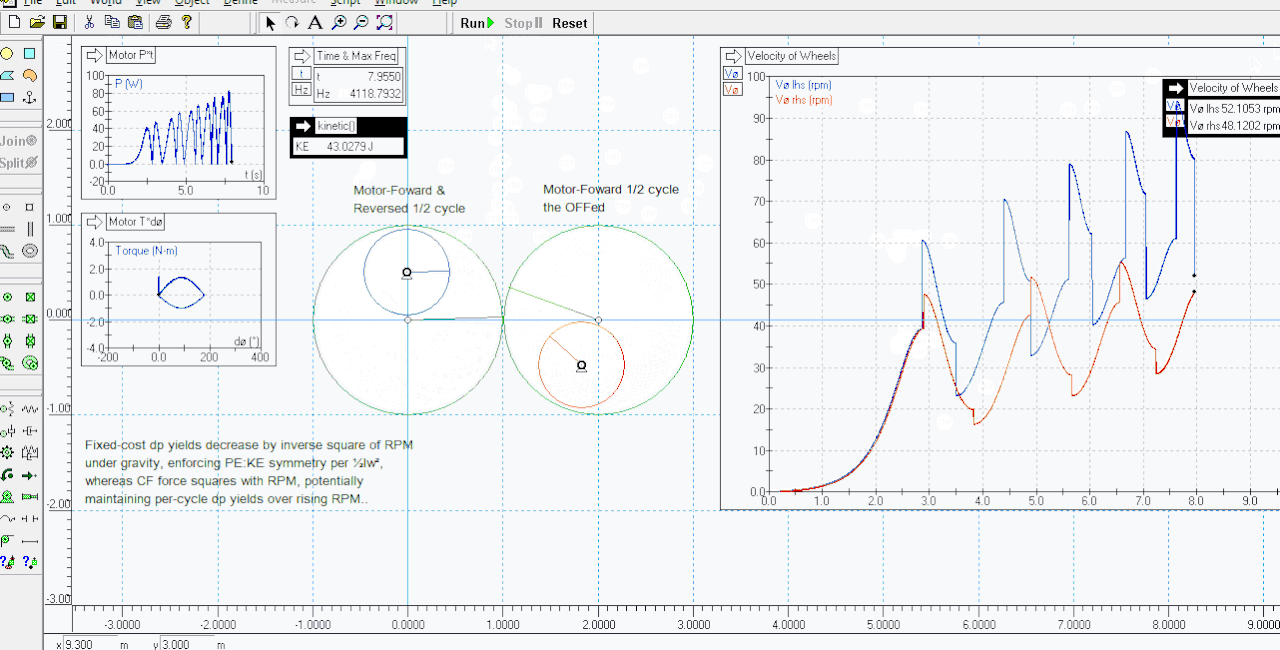
In the current crude application, a heavy flywheel is attached to the main wheel at fixed radius, thus overbalancing it and causing it to keel under gravity, and this is mounted via a motor. The motor is then controlled for 'velocity' using the following instruction:
Code: Select all
"if(body[5].p.x<0,body[1].v.r,-body[1].v.r)" In other words, if the flywheel's on the left side of the 0,0 origin at the wheel's axis - thus descending - then the motor turns the flywheel in the same direction and at the same speed as the wheel itself. The resulting counter-torques from this acceleration slow down the drop, prolonging the OB weight's exposure time to gravity's constant acceleration, and so increasing the momentum yield available from the given weight and height.
Passing BDC onto the right side of the axis, the torque sign is reversed and the flywheel spins down, thus unloading its stored momentum back into the wheel axis and so accelerating the lift, reducing its dwell time under gravity's constant deceleration, and so reducing the amount of gained angular momentum that must be shed back to gravity and time, consolidating this boosted per-cycle momentum yield over a succession of five full cycles.
The ratio of KE gain to work performed by the motor is then measured by two different metrics - power x time and force x displacement - at sufficient accuracy to resolve the interaction down to millijoule noise levels. In principle, anyway - the last attempt, MTM4, exhibited a rare failure to resolve consistently, hence this further development of the core idea; the possibility that CF force may offer a proxy for accessing RPM-invariant momentum gains from gravity and time.
The problem this is trying to address is the fact that all else being equal, drop times and thus G*t yields decrease inversely to RPM - the faster the wheel turns, the less momentum is gained from each identical lift and drop of the OB cycle. So your GPE never changes, but the amount of fresh angular momentum it's worth each cycle is decreasing inversely to the square of RPM - at 10X the speed the OB weight spends one-tenth the time under gravity's constant acceleration.
CF force however also squares with RPM, hence at 10x the speed we'd have access to 100x the effective g-force. Surely this could help redress the dwindling momentum returns as RPM's rise?
..and i know what you're thinking; if the CF force is squaring with RPM then wouldn't the cost of momentum also? No! Because we're not performing work against CF force, strictly speaking; we're not even performing work against gravity: the only workload, again, being accelerating and decelerating angular inertia. This seems an eminently conservative exchange - for instance if we accelerate the flywheel by 1 rad/s relative to the main wheel, and then decelerate it back to relative stasis, then almost the same amount of work has been output as input - it's virtually the same torque times angle in each direction, minus the small per-cycle KE gain.
The motivating principle here is simply the fact that it costs ½ J to accelerate 1 kg-m² by 1 rad/s from a standing-start, regardless of the absolute system RPM; doesn't matter if the wheel's stationary or else already turning at 10 rad/s, half a joule of work will produce a 1 rad/s relative speed difference between the 1 kg-m² flywheel and main wheel. This is obviously conducive to the objective of RPM-invariant momentum costs.
So with these points in mind, here's a first draft of what this interaction currently looks like:

Note that the net displacement between the two parts remains zero; the flywheel's effectively oscillating, but precisely because the relative speed isn't increasing, neither is the input workload or its associated energy cost.
The reason why everything in a true PMM must, of necessity, go around together - the EMGAT principle - is that the energy cost of momentum sourced from pushing against a stator inevitably squares with the squaring distance over which that force must be applied in order to continue accelerating, this being the practical factor enforcing PE:KE symmetry. Thus the benefit of a stator you can take with you is in preventing that cost from escalating; again, a 1 rad/s relative acceleration of 1 kg-m² always costs half a Joule from relative stasis, no matter the current system angular velocity.
The torque over angle plot is obviously immediately interesting in this respect - each cycle tracing the identical T*a - ie. performing the same, unchanging workload - invariant of the accumulating system RPM's..
Bear in mind that the intention was to mount such a system inside a larger wheel, replacing real gravity with centrifugal force; the thinking being, that as CF force squares with RPM, this will be equivalent to gravity increasing with RPM, thus potentially cancelling out the usual diminishing momentum returns with rising RPM's, whilst fixing the unit-energy cost of those momentum gains to a constant per-cycle value. OU would then develop as the difference between the final KE value versus the sum of the per-cycle cost times the number of elapsed cycles. I still intend to try this.
But something else has come up.. something unexpected: that rig you see above, the one temporarily using gravity? Yup. Consistently. Always positive, never negative.
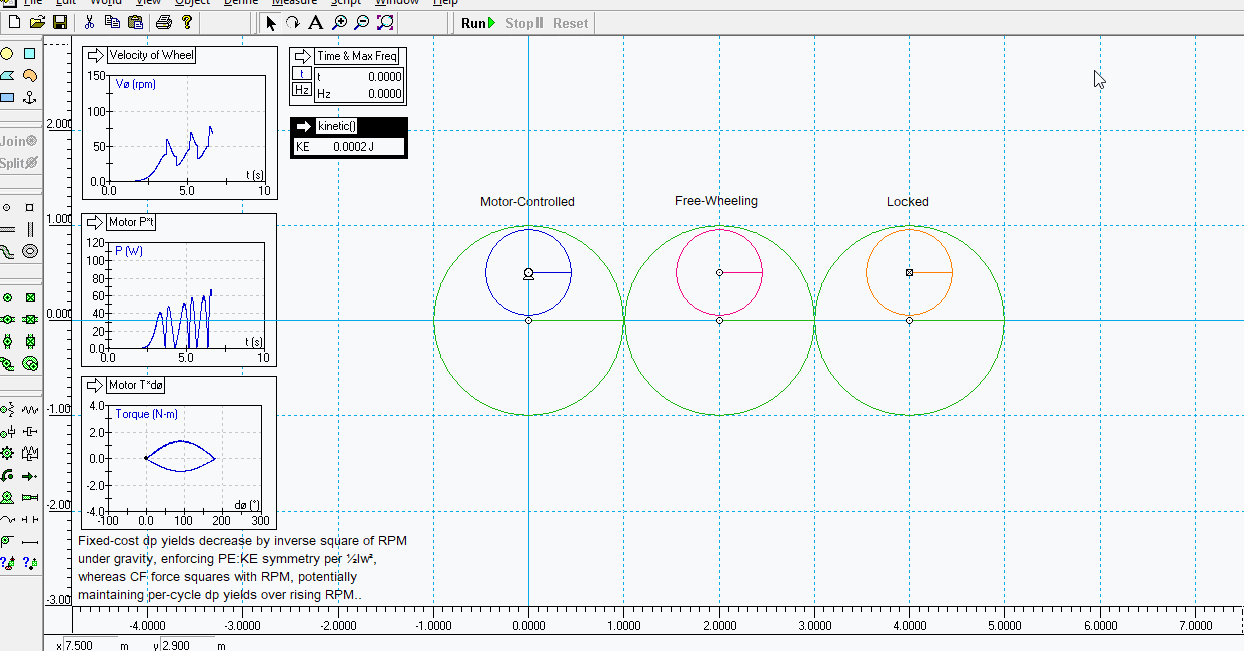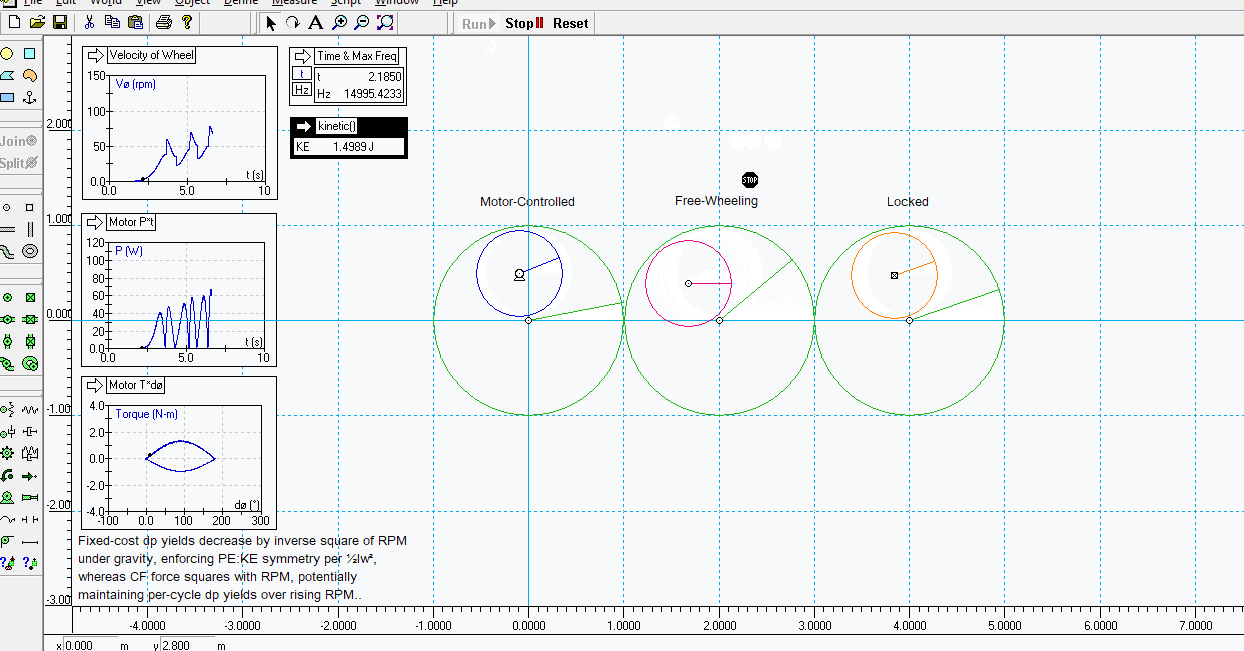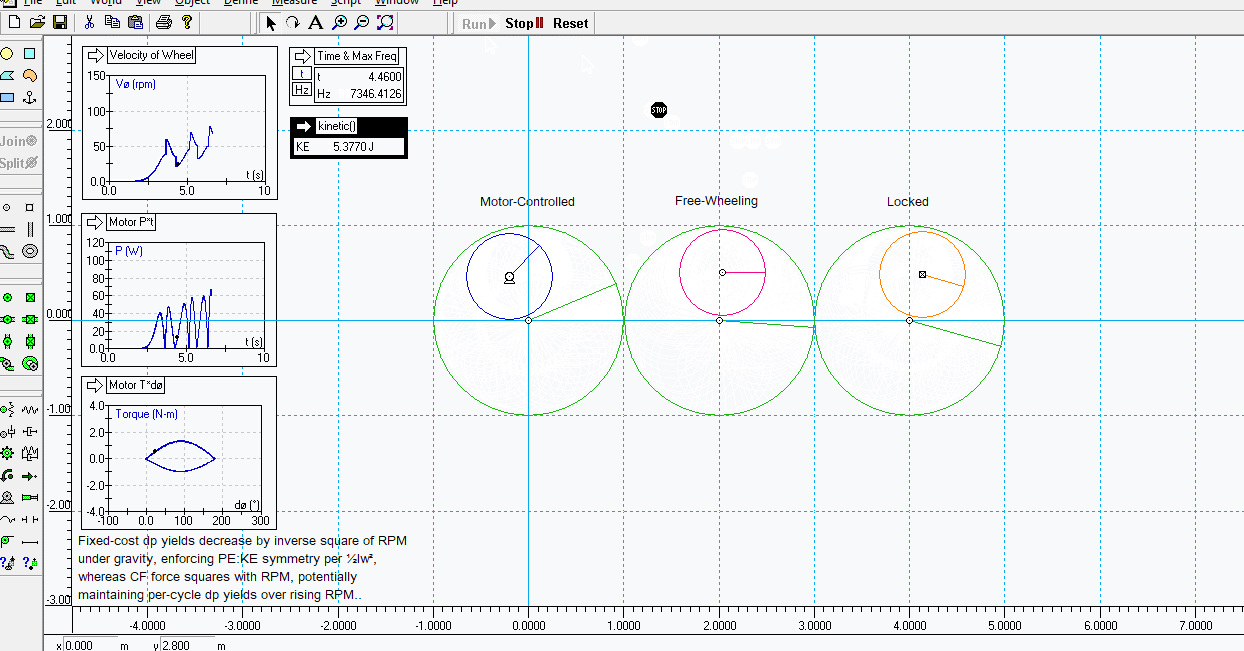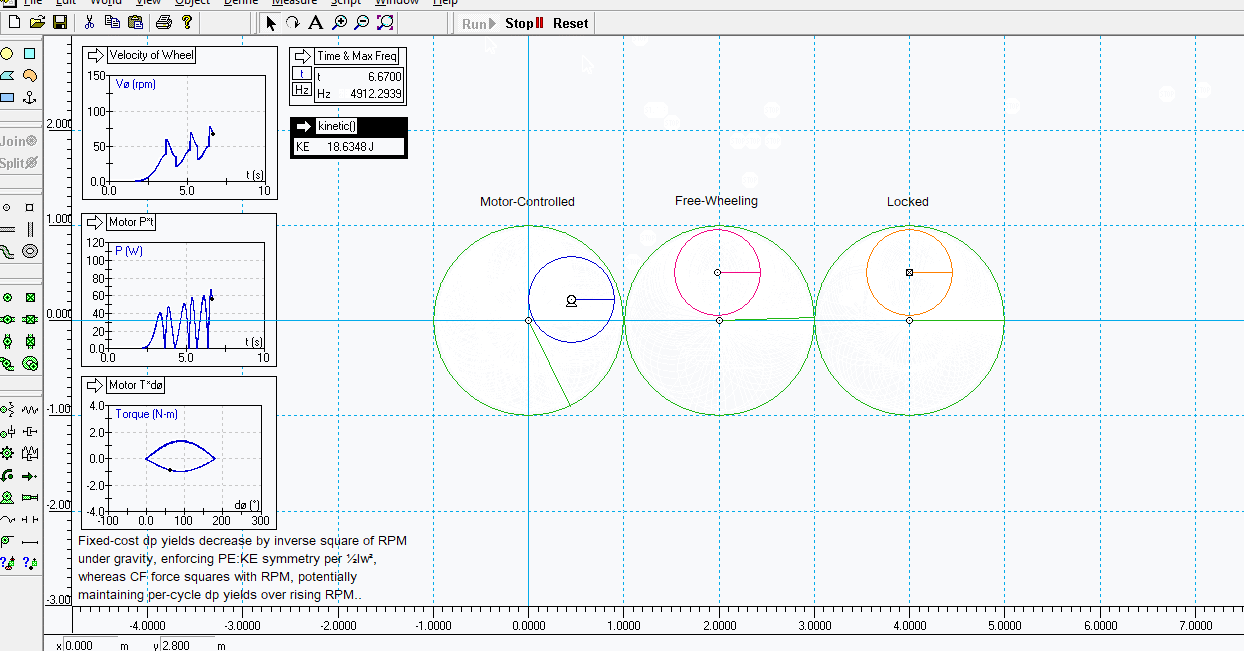
The first run made 32 J, with the input metrics coming out like this:
P*t = 23.62619071
T*a = 23.62614435
Sub-millijoule agreement there. I reduced the initial small kick of energy given to it to cause it to topple over in the right direction to a negligible amount, and lowered the integration error to 1e-20 with variable integration steps, managing to get the KE rise for the same five cycles down to 27.45 J (as in the sim seen above), for this cost:
P*t = 24.21164033
T*a = 24.21162772
..again, sub-millijoule agreement, apparently showing a PE discount far above noise levels (four sigma?).
The interaction's simple enough anyone can model it themselves - deploy counter momenta to slow down the drop and speed up the lift, aiming for zero net relative displacement between the two parts, and measure its efficiency over rising RPM..
I'm gonna plough ahead and mount one of these under G-force instead of real gravity - i expect i'll use a motor to turn the system and produce the CF force initially, rather than an OB system; all i really need to know for now is how efficiency evolves as a function of rising G-force, ie. does this compensate the usual diminishing dp/dt returns of increasing angular velocity, and if so how does its cost sum over successive cycles and rising RPM? But even at this early stage, the principal appears to be gaining energy under ordinary gravitation..
Anyone out there yet to indulge the joys of cutting and pasting 32k lines of data into a spreadsheet Riemann sum, today is your day; this needs independently verifying ASAP..