MrVibrating wrote:It's like i'm showing you the plans for a hydro-electric dam, and you're all like "but it's just a big wall, how's that make energy? All that concrete must cost a bit?"...
You have to admit that building a hydroelectric dam wall in the middle of the desert sounds a bit strange.
Perhaps you could also provide a basin, a good weather prediction and/or an additional mountain...
Because you sure ignore the influx of energy: A continuous source of water in the metaphor, and for the mechanism it is that programming effect of the actuators.
But I don't care if you build a big wall and hope for rain. Who actually knows what will happen, and how much foresight you have.... I just provide a scribble in the sideline for the silent readers -- who have their own, perhaps totally different, opinion.
Moving masses in and out cannot add any momentum - on the contrary, it conserves it.
Agreed.
But such conservation stuff is not the case in your experiment.
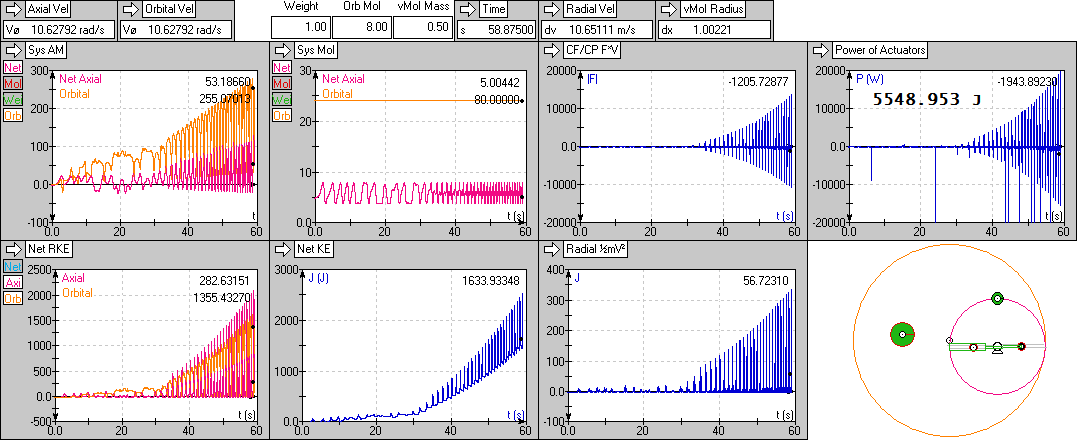
The actuator is just programmed to move no matter what, why and how... (how fast it's able to react, how much it needs to accelerate, how much energy it would cost, where to get it from. Via the one-line-programming of the actuator position there is absolutely no mechanical environment to counter its action: like when the radial motion would be mechanically controlled and coupled by a gear, a lever or a pulley etc. It just bluntly moves in synchronization with the rotation of the wheel. The energy gains and requirements are completely in the dark.
Hence, on page 2, I replaced your motor with a spring in order to help enlighten the physics behind it.
Feel free to ignore. But the claims of any kind of gain is false.
We have a similar (but slightly different) situation here:
http://www.besslerwheel.com/forum/viewtopic.php?t=7636
Big Gains, At a Complete Loss..
On page 3 the result of a spreadsheet physics solver...
---
You cannot add angular momentum to a system via MoI variations alone, period. They can only vary the KE.
But you just add angular momentum directly by forcing your actuator motion against the centrifugal and gaining kinetic energy is exactly what you observe.
When you'd observe where you need the most energy to move at your desired speed at your desired radial distance, then you'd see it's simply on that ascending side. Your actuator just does the energy-adjustment automatically because it just moves to a predefined location, you assume it doesn't matter...
Only gravity can contribute momentum, because it is a uniform acceleration
Dude..?
For your reference, consider again what happens when the two interactions are rotated 90° relative to one another:
Much appreciated !
They are symmetric.
No longer are the red angular weights on the outside when the Green pendulum goes down, and no longer on the inside when the green goes up.
hmm. ok I see.
I notice I'm biased to see exactly what I tried to show in "Importance of raising weights"...
I just see similar things: To me a vertical raise against gravity is similar (not equal) to a center seeking raise against centrifugal.
Perhaps that view is not entirely normal... SORRY.
Your latest example is as like moving sideways (as people usually try in their PMM).
Hence it is most likely that when you reverse this latest action (as if like moving towards the unfortunate ascending side), the effect will be even worse.
But that similarity doesn't change a thing, actually makes it easier.
In my topic I'm not talking about any mechanism, just about the necessity of a lift to create an overbalanced situation, and thus the futility to move sideways as is usually attempted. In my case I could use an actuator to raise things against gravity, doing it 180 degrees apart it also continuously moves back and forth... such action costs energy, and is equalized with the resulting torque per cycle: (wheel acceleration)
I have to admit, rising against centrifugal is perhaps more elegant.