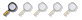I'd been intending to plonk the second rotor + motor in the middle of the OB one, like this:

..so that new dark blue rotor would have the same MoI as the OB rotor. Pretty straightforward, however, it's
increasing the net weight of the system..
..whereas, note that the system
already contains an unused internal axis; that of the weights themselves! So, why not just use
that instead - increase the radii of the weights so that their summed MoI's are equal to to that of the main axis? Like this:

Whilst slightly more
visually complex, it's
physically leaner & more elegant..
So now, each weight still has a mass of 0.125 kg, but also a radius of sqrt2 meters, giving each an axial MoI of 0.250 kg-m² (per MoI=mr²)... so a net MoI of '1' in both the over-balancing and 'spin-up & brake' axes, and obviating the need for the extra weight of a dedicated second rotor..
If the end results prove negative, i'll maybe re-try using a dedicated second rotor after all, since more mass for a given speed means more energy.. (ie. i might've just inadvertently eliminated a key gain condition there, but we'll see.)
It'll now need four motor + brake sets instead of just the one, but they'll all run exactly the same instructions in perfect sync, so it's no more complex to sequence. Also, note that the masses and MoI's of each motor's 'stator' and 'rotor' halves, along with those of the 'brake discs' and 'calipers', can be included into those of the
present masses and MoI's - so the motors and brakes themselves need add no additional mass or inertia.
• This same point applies to the MoI's of any switches / wires / sensors / nuts & bolts etc. in a real build - if 'everything must go around together', then everything with mass is contributing MoI.. but so long as the
net ratio of the two interacting MoI's in the 'accelerate & brake' cycle is 1:1 (whatever their individual compositions),
that's the shortest, neatest route up the OU ladder.. assuming a successful N3 break of course.
So, the next step is to add the four motors & brakes, plus their meters, then set the target relative speed with an input control field or slider (lower relative target speed = faster 'spin-up & brake' frequency and vice-versa, interesting dynamic to play with), and we should be good to go..
..as an afterthought, it might also be worth including an input control field / slider for the ratio or percentage of applied motor torque relative to the constant OB torque, to allow for runs with partial counter-torque cancellation instead of just fully cancelling..
..also, the previous "acceleration" plot wasn't particularly useful info on its own; 'OB torque' would be better, but WM
cannot measure the OB torque at its axis because..
it's not there! It's coming
from gravity.. so WM has no means to meter it directly (or, thus, any corresponding counter-momenta).. so i've now applied N2 to get the OB torque over angle instead (per F=mA, T=MoI*rad/s²). So now it's possible to measure and compare the
T*a work integral actually output by gravity, with the rotational KE rise as a function of half the MoI of the OB axis times its speed squared, and in relation to the actuator and rotary solenoid input integrals.
As an additional benefit, this instantaneously-derived 'OB torque' value can be
fed back to the motors, so their applied counter-torque will always be perfectly matched / scaled to it..
Finally, before progressing straight to the spin-up & brake cycles, it'd probably be worth just checking that the system
as-is can solve reliably to within a millijoule or so of unity (ie.
not because there's any chance of an anomaly, but precisely because there can't be). Call it a baseline 'dry run':

..and aside from the tiny implied 'gain' on the rotary solenoids (almost certainly noise from the reactive feedback process caused by coarsely-tuned multipliers), it's nigh-on perfect.
So the system's ready to start making KE.. by cyclically spinning up and then braking the weights themselves!
As ever, the question is not whether the four motors will show OU - we already know that's guaranteed - but whether or not the 'gain' will be equal to the input energy drawn by the OB system..