I think i might be starting to see something, a path forwards perhaps..
There's a potential momentum source that i haven't yet managed to test:
• suppose we could apply a linear force, downwards, upon the axle / support posts, in propelling a mass upwards
So we've raised some 'upwards' linear momentum, against the inertia of the Earth.
• now suppose it gets up so high, before gravity pulls it back down again, landing on the OB side of the wheel..
The key point is that the linear-to-angular conversion is accomplished by gravity,
without incurring a counter-torque component within the wheel system.
Thus an otherwise inertially 'closed' rotating system is continually being fed with more fresh angular momentum, converted by gravity and raised
as linear momentum against Earth.
I don't know yet a) whether this is actually possible (the linear-to-angular conversion), nor b) if it would furnish fixed-cost momenta in spite of rising RPM.
However, now that you have the general picture of what i'm considering, it seems to follow as a consistent train of logic in the latter pages of MT (even assuming they're in preserved order, always in question); beginning with MT 132:

..linear inertial interactions against the axis / earth, featuring a square hub.
Now 133:

..main feature: dropping weights in the rotating frame in order to pump some fluid against the terrestrial frame..
..insert: that 'fluid' now a 'pound-weight' being accelerated & raised
against the axis - ie. levering the pound-weight upwards by pushing the earth downwards..
..on to 134:
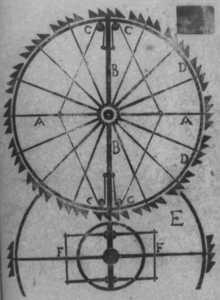
- main feature = same deal; angular displacements in the rotating FoR leveraging linear displacements against the axis / earth, now depicting the inputs divided into 'four quarters'
- insert = a kind of Roberval planar linkage for doing the same thing
135:

..
any linear displacement thru the fixed axis is still a linear inertial interaction with the earth - if a pole is thrust upwards, the earth is thrust downwards via the axis..
136:

..but how to convert these linear momenta into
angular..?
Now, note here in this scan of MT that '143' actually
precedes '137':

..so
first we see "
pounds in equilibrium" (hence a potential visualisation for "pounds" in the 'part 1 riddle' - and again using a Roberval-type planar linkage..
..and
then, 'MT137' - the most immediate impression being that is represents a multiplied schematic of this same Roberval-type angular-linear linkage..
Culminating in the Toys page, MT 138-141:

..so if that
is a thread of continuity, the lower hammer toy 'D' is raising linear momentum against the 'square' hub (ie. the earth via the fixed axis), and affirmed via the alignment of the lower toy mid-way between the left and right notches on 'B', representing the system axis - ie. this initial linear acceleration
does not apply torque or counter-torque to the axis..
The scissorjack, culminating in 'one quarter', represents the linear-to-angular conversion of that momentum as it is given to the OB weights represented by the upper toy 'C', and resulting in the accumulating clockwise v counter-clockwise momentum asymmetry represented by 'A'.
The upturned whistling top - by dint of being upside-down - implying a
linear, as well as angular, interaction with the earth..
So to briefly resummarise: besides kiiking and 'classic OB', perhaps a 3rd way to gain 'statorless' momentum is by converting linear momentum applied against the fixed axis to earth, into angular momentum, via gravity. I don't yet know however if this is possible, much less if it offers opportunity for trapping momenta at RPM-invariant efficiency..
However with regards to 'the riddle', suppose it
did allude to an effective energy asymmetry..
• to "lightly" cause a heavy weight to fly upwards
..puts 'lightly' in scare-quotes; there's a reservation involved,
contingent upon something..
If 4 'ounces' fall while 1 lb rises equal height - an effective GPE asymmetry but stay with me - then a) we're talking about an
input energy discount, rather than excess output - so, logically consistent with the actual implicit physics of OU - and b) that discount can only be due to the 'ounces' being in an anomalously-accelerated reference frame; that is, one that is not inertially interacting with its environment, or, thus, exchanging counter-momentum with it; furthermore if the output value of that input workload is being raised by a factor of 'four', then the relative velocity delta between I/O FoR's must be a factor of two - that is, the absolute accelerations of the 'ounces' is twice as high, in the ground FoR, as the actual work being performed in the anomalously-accelerating rotating FoR.
Hence a pound weight might be accelerated upwards against a
full compliment of linear counter-momentum transferred to earth via the support posts, yet "lightly" with respect to the axis of rotation, since no counter-torque has been applied..!
An effective reactionless angular acceleration of four 'ounces' of GPE in a rotating FoR might, thus, conceivably, raise 'one pound' of GPE in the ground FoR..
Little sketchy perhaps, but does frame a specific type of interaction that can be further investigated; namely, trying to get gravity and rotation to stably convert linear into angular momenta, and
then, without the input work each cycle having to increase with rising RPM..








