Blood From Stone
Moderator: scott
re: Blood From Stone
Thanks as always dax .. the next paragraph.
"(Page 64) ... , so I too am pleased to reflect that others, likewise through His goodness, possess a greater talent for analysing and describing, more artistically that I, this soon-to-be-revealed mystery ..."
Dang .. seems he thought others might be better able to analyse and drill down deeper than he could to describe his mechanical principle.
Side Rant : Surely in this age of the internet, our instant communications, sharing of information, libraries at the end of a fingertip, textbooks freely available, simulation programs, we would stand a better than good chance of finding a physical mechanical principle that Bessler thought someone else could do a better job of analysing.
"(Page 64) ... , so I too am pleased to reflect that others, likewise through His goodness, possess a greater talent for analysing and describing, more artistically that I, this soon-to-be-revealed mystery ..."
Dang .. seems he thought others might be better able to analyse and drill down deeper than he could to describe his mechanical principle.
Side Rant : Surely in this age of the internet, our instant communications, sharing of information, libraries at the end of a fingertip, textbooks freely available, simulation programs, we would stand a better than good chance of finding a physical mechanical principle that Bessler thought someone else could do a better job of analysing.
-
MrVibrating
- Addict

- Posts: 2879
- Joined: Sat Jul 31, 2010 12:19 am
- Location: W3
I just tried a simplified version of the above hypothesis:
- after the 1st cycle, i doubled the radius of the wheel, making it 2 meters
- per MoI=mr^2 this quadruples the MoI, hence quartering the RPM and thus RKE
- so we go from 40 J of RKE down to 10 J, the other 30 J "loaded into an onboard spring"
- the motor then performs another 40 J of work as before, over 1 complete cycle.
- this raises the angular momentum from 89 p up to 200 p:
cyc#2 begins with 89.6828 p, ends with 200.5252 p, so a yield of 110.8424 p
So we actually netted even more momentum on the 2nd cycle than the 1st, for the same 40 J of work.
No sign of OU tho (surprise) - the cycle begins with 10 J of RKE, rising to 50 J, plus the 30 J of PE stored in the notional spring, so 80 J all-up from two 40 J input workloads.
So what's useful and what's not, here?
We can evidently control the per-cycle momentum yield, by dynamically raising MoI and thus reducing RPM, and so increasing the effective duty-cycle, in spite of rising system momentum.
With careful control, we could pay identical input energy for identical quotas of momentum per cycle, for a consecutive number of cycles, limited only by sheer size constraints..
..however with things as they are, output energy is obviously not diverging from input energy.
Why? Which boxes on the OU T's & C's haven't been ticked?
The problem here is the type of workaround applied - reducing speed to play for time is precluding the very manifestation of the higher-speed energies we're after. Accumulating reactionless momentum only causes OU if the velocity component is accumulating...
..cranking up the inertia component instead is just useless, cargo-cult engineering - the whole point of accumulating momentum is to accelerate the reference frame, so that 10 J of PE performs 50 J of work, or whatever - yet here i'm just hoarding momentum for its own sake, irrespective of its velocity and thus KE / PE symmetry.
In conclusion, this is a wrong turn, chasing the right ends, but by the wrong means.
The core weakness is that the motor speed has to increase, in counter-rotation to the wheel, as system RPM's rise. This condition precludes OU right from the outset.
For OU to emerge, the reference frame of the stator has to be accelerating with the rest of the system.. not away from it.
This obviously implies that collisions - especially inelastic ones - are an absolutely essential ingredient..
..in timely reminder tho, collisions for collisions sake are as useless as hoarding reactionless momentum for its own sake - collisions are only essential insofar as a means of completing a reactionless acceleration.
So for example:
- a force is applied between two inertias, somehow only accelerating one of them
- the accelerated mass and non-accelerated mass then collide, consolidating that lone momentum rise back into a net system rise
..rinse & repeat.
So, at a fundamental level, we're looking for a different stator trajectory.
Not a counter-rotating one.
It has to terminate in some kind of collision, resulting in a net acceleration of the complete system.
A motor locking its position at a given angle (as used in the above tests) is sufficient for such a collision, however we currently don't know if the optimum dimensions for the input force required are angular or linear. This boils down to the question of what forms the 'stator' - could it be a radially-moving mass, an angular motion, some combination? Does it require a period of 'freefall'?
The most likely explanation screaming off the page seems to be that the 'stator' is some kind of transiently-gravitating mass. Torque is applied between it and the rotor, whilst it is gravitating, hence effectively causing the reference frame of the input workload to diverge into the 'freefall' reference frame.
This is followed by a soft collision, equalising the speed difference between them again.
Then the process is repeated.
Yet in all variations on this so far tried, the energy gain comes at the expense of GPE..
It's fairly trivial to torque up a rotor against a falling 'stator'. And indeed, we can watch in wondrous amazement as 10 J magically transforms into 50 J of work..
..except we now have a 40 J GPE deficit, repaid by relifting the stator-weight. Net result is energy unity - we do get a 'reactionless' momentum rise, but the energy efficiency never diverges from ½mV².
The trick i'm missing has to involve variable MoI - that's the only wildcard on offer. But how and when to play it?
- after the 1st cycle, i doubled the radius of the wheel, making it 2 meters
- per MoI=mr^2 this quadruples the MoI, hence quartering the RPM and thus RKE
- so we go from 40 J of RKE down to 10 J, the other 30 J "loaded into an onboard spring"
- the motor then performs another 40 J of work as before, over 1 complete cycle.
- this raises the angular momentum from 89 p up to 200 p:

cyc#2 begins with 89.6828 p, ends with 200.5252 p, so a yield of 110.8424 p
So we actually netted even more momentum on the 2nd cycle than the 1st, for the same 40 J of work.
No sign of OU tho (surprise) - the cycle begins with 10 J of RKE, rising to 50 J, plus the 30 J of PE stored in the notional spring, so 80 J all-up from two 40 J input workloads.
So what's useful and what's not, here?
We can evidently control the per-cycle momentum yield, by dynamically raising MoI and thus reducing RPM, and so increasing the effective duty-cycle, in spite of rising system momentum.
With careful control, we could pay identical input energy for identical quotas of momentum per cycle, for a consecutive number of cycles, limited only by sheer size constraints..
..however with things as they are, output energy is obviously not diverging from input energy.
Why? Which boxes on the OU T's & C's haven't been ticked?
The problem here is the type of workaround applied - reducing speed to play for time is precluding the very manifestation of the higher-speed energies we're after. Accumulating reactionless momentum only causes OU if the velocity component is accumulating...
..cranking up the inertia component instead is just useless, cargo-cult engineering - the whole point of accumulating momentum is to accelerate the reference frame, so that 10 J of PE performs 50 J of work, or whatever - yet here i'm just hoarding momentum for its own sake, irrespective of its velocity and thus KE / PE symmetry.
In conclusion, this is a wrong turn, chasing the right ends, but by the wrong means.
The core weakness is that the motor speed has to increase, in counter-rotation to the wheel, as system RPM's rise. This condition precludes OU right from the outset.
For OU to emerge, the reference frame of the stator has to be accelerating with the rest of the system.. not away from it.
This obviously implies that collisions - especially inelastic ones - are an absolutely essential ingredient..
..in timely reminder tho, collisions for collisions sake are as useless as hoarding reactionless momentum for its own sake - collisions are only essential insofar as a means of completing a reactionless acceleration.
So for example:
- a force is applied between two inertias, somehow only accelerating one of them
- the accelerated mass and non-accelerated mass then collide, consolidating that lone momentum rise back into a net system rise
..rinse & repeat.
So, at a fundamental level, we're looking for a different stator trajectory.
Not a counter-rotating one.
It has to terminate in some kind of collision, resulting in a net acceleration of the complete system.
A motor locking its position at a given angle (as used in the above tests) is sufficient for such a collision, however we currently don't know if the optimum dimensions for the input force required are angular or linear. This boils down to the question of what forms the 'stator' - could it be a radially-moving mass, an angular motion, some combination? Does it require a period of 'freefall'?
The most likely explanation screaming off the page seems to be that the 'stator' is some kind of transiently-gravitating mass. Torque is applied between it and the rotor, whilst it is gravitating, hence effectively causing the reference frame of the input workload to diverge into the 'freefall' reference frame.
This is followed by a soft collision, equalising the speed difference between them again.
Then the process is repeated.
Yet in all variations on this so far tried, the energy gain comes at the expense of GPE..
It's fairly trivial to torque up a rotor against a falling 'stator'. And indeed, we can watch in wondrous amazement as 10 J magically transforms into 50 J of work..
..except we now have a 40 J GPE deficit, repaid by relifting the stator-weight. Net result is energy unity - we do get a 'reactionless' momentum rise, but the energy efficiency never diverges from ½mV².
The trick i'm missing has to involve variable MoI - that's the only wildcard on offer. But how and when to play it?
- cloud camper
- Devotee

- Posts: 1083
- Joined: Tue Mar 15, 2011 12:20 am
re: Blood From Stone
Yup, smooth mathematical curves in weight motions are never going to work - this is the very definition of mathematical symmetry.
What we need is a step function in the weight motions that allow for a symmetry break at the step. This is where the collisions come into play - possibly allowing one to sidestep the height for width conundrum.
Again, smooth continuous motions controlling weight motions are the very definition of symmetry! And mathematical symmetry means that all energy conservation laws are religiously followed.
Without a step fuction all we accomplish is a smooth 1/1 conversion of GPE to RKE and back again.
Mathematicians will tell you that the only place interesting behavior occurs is at boundary conditions of functions as this is where the math breaks down and no longer produces smooth predictable output.
The solution will probably not be found in a simulator as the necessary step function cannot be defined by mathematics, only mechanically by a physical mechanism.
What we need is a step function in the weight motions that allow for a symmetry break at the step. This is where the collisions come into play - possibly allowing one to sidestep the height for width conundrum.
Again, smooth continuous motions controlling weight motions are the very definition of symmetry! And mathematical symmetry means that all energy conservation laws are religiously followed.
Without a step fuction all we accomplish is a smooth 1/1 conversion of GPE to RKE and back again.
Mathematicians will tell you that the only place interesting behavior occurs is at boundary conditions of functions as this is where the math breaks down and no longer produces smooth predictable output.
The solution will probably not be found in a simulator as the necessary step function cannot be defined by mathematics, only mechanically by a physical mechanism.
re: Blood From Stone
"Blood from Stone"
That's an apt description for our combined attempts to rediscover Bessler's mechanical PM principle, the foundation for his Laws of PM.
We coax, cajole, prod, massage, bully, harass, and bludgeon the Laws of Physics and byzantine mechanical principles, attempting to wring out of them the so simple, yet so deeply hidden mechanical answer to his everlasting motion, to plagiarize him.
Fair Warning : .. I'm going to keep rattling the cage, at least a little while longer. It is for everyone to decide what is the truth and the path they will take, as we have always done. For those already on a particular path this is to provide perhaps another perspective.
We as humans of this age imo are perhaps uniquely constrained in our quest to discover Bessler's 'artistry'. We are regimented and somewhat linear in our thought processes. I'll give you an example. I use a sim program almost exclusively these days. I have quite a good working knowledge of the math and relationship symmetry of those same Newtonian Laws behind the sim program. I love to use it for design and to test actions against what I imagine something will do. Yet I am constrained to the limits of that program. What I sometimes think is artistry in my designs is nothing more than following rules. Well prescribed and tested rules I might add. Bessler did not have a sim program, he probably didn't have a superior working knowledge of Newton's Laws, most certainly not to the combined level of the thousands of engineers who designed, built, and Beta tested the sim program. So an in-depth knowledge of the Laws of Physics and the math behind them is not a prerequisite to discover Bessler's 'artistry'. In fact I'd say the answer does not lie there in the least, except to exercise our neurons. Whether we examine fine boundary conditions or not.
We collectively and individually perhaps lack the perspective that Bessler eventually found. No one can say Bessler was a just a PM weekend warrior. He gave it everything and he built multiple OOB designs over 10 years. He tried gravity, wind and water, and combinations of same. They didn't work, not one. I can well imagine him toiling away on his latest OOB design right up to the moment he had his dream, his epiphany. Then a wider perspective came to him, a right-brain coup over logical left-brain, outside the fringes of his previous thinking, where he saw a way forward at last. Perhaps a change in use for an OOB system, perhaps an addition of another structure to his OOB system that became the Prime Mover proper, along with the ubiquitous connectedness principle. It worked, and his 'artistry' had triumphed over his pure logical mechanical ability, to birth 'everlasting motion' and his true PMM.
He found it where everybody else had looked - tick.
He could on paper calculate Inputs to Outputs (the mathematical simplicity); however he thought others could better analyse and describe his 'artistry' than he. i.e. he saw the cause and effect science of a turning wheel, and he could describe and analyse it down to a level of accumulating momentum and excess impetus. Beyond that the detail was for the mathematicians.
You might dismiss my Sunday musing as a fiction, delusional, nothing but for entertainment value on a slow day. Maybe so, then again ..
That's an apt description for our combined attempts to rediscover Bessler's mechanical PM principle, the foundation for his Laws of PM.
We coax, cajole, prod, massage, bully, harass, and bludgeon the Laws of Physics and byzantine mechanical principles, attempting to wring out of them the so simple, yet so deeply hidden mechanical answer to his everlasting motion, to plagiarize him.
Fair Warning : .. I'm going to keep rattling the cage, at least a little while longer. It is for everyone to decide what is the truth and the path they will take, as we have always done. For those already on a particular path this is to provide perhaps another perspective.
We as humans of this age imo are perhaps uniquely constrained in our quest to discover Bessler's 'artistry'. We are regimented and somewhat linear in our thought processes. I'll give you an example. I use a sim program almost exclusively these days. I have quite a good working knowledge of the math and relationship symmetry of those same Newtonian Laws behind the sim program. I love to use it for design and to test actions against what I imagine something will do. Yet I am constrained to the limits of that program. What I sometimes think is artistry in my designs is nothing more than following rules. Well prescribed and tested rules I might add. Bessler did not have a sim program, he probably didn't have a superior working knowledge of Newton's Laws, most certainly not to the combined level of the thousands of engineers who designed, built, and Beta tested the sim program. So an in-depth knowledge of the Laws of Physics and the math behind them is not a prerequisite to discover Bessler's 'artistry'. In fact I'd say the answer does not lie there in the least, except to exercise our neurons. Whether we examine fine boundary conditions or not.
We collectively and individually perhaps lack the perspective that Bessler eventually found. No one can say Bessler was a just a PM weekend warrior. He gave it everything and he built multiple OOB designs over 10 years. He tried gravity, wind and water, and combinations of same. They didn't work, not one. I can well imagine him toiling away on his latest OOB design right up to the moment he had his dream, his epiphany. Then a wider perspective came to him, a right-brain coup over logical left-brain, outside the fringes of his previous thinking, where he saw a way forward at last. Perhaps a change in use for an OOB system, perhaps an addition of another structure to his OOB system that became the Prime Mover proper, along with the ubiquitous connectedness principle. It worked, and his 'artistry' had triumphed over his pure logical mechanical ability, to birth 'everlasting motion' and his true PMM.
He found it where everybody else had looked - tick.
He could on paper calculate Inputs to Outputs (the mathematical simplicity); however he thought others could better analyse and describe his 'artistry' than he. i.e. he saw the cause and effect science of a turning wheel, and he could describe and analyse it down to a level of accumulating momentum and excess impetus. Beyond that the detail was for the mathematicians.
You might dismiss my Sunday musing as a fiction, delusional, nothing but for entertainment value on a slow day. Maybe so, then again ..
re: Blood From Stone
Fletcher, thanks.
A thought provoking Sunday morning SERMON.
Raj
A thought provoking Sunday morning SERMON.
Raj
Keep learning till the end.
- John Collins
- Addict

- Posts: 3299
- Joined: Wed Nov 05, 2003 6:33 am
- Location: Warwickshire. England
- Contact:
re: Blood From Stone
Excellent commentary Fletch. As you know I’m not a fan of sim programs, although I was grateful for your efforts on my behalf, I have always found that for me at least, the intuitive process which develops from building models is more likely to lead to success than simply designing from a sim.
The trouble is, IMO, you can picture a design in your mind and on paper and set the sim to test it, and that’s one design tested, but when you build, all kinds of variations come into your mind which you can test manually before you complete the build.
I am, of course, a complete dunce where sims are concerned so I’m bound to think like that, but on the other hand, intuitively, I just know that the solution will only come from a builder. Having said that, I still believe that Bessler’s wheel will prove to be testable with a sim, but that solution will not derive from a simulated design.
That sounds contradictory, but what I mean is that any sim will successfully test a design, as long as the correct and accurate information is input because the sim works according a set of rules, as you suggested Fletch.
I hope this makes sense?
JC
The trouble is, IMO, you can picture a design in your mind and on paper and set the sim to test it, and that’s one design tested, but when you build, all kinds of variations come into your mind which you can test manually before you complete the build.
I am, of course, a complete dunce where sims are concerned so I’m bound to think like that, but on the other hand, intuitively, I just know that the solution will only come from a builder. Having said that, I still believe that Bessler’s wheel will prove to be testable with a sim, but that solution will not derive from a simulated design.
That sounds contradictory, but what I mean is that any sim will successfully test a design, as long as the correct and accurate information is input because the sim works according a set of rules, as you suggested Fletch.
I hope this makes sense?
JC
Read my blog at http://johncollinsnews.blogspot.com/
This is the link to Amy’s TikTok page - over 20 million views for one video! Look up amyepohl on google
See my blog at http://www.gravitywheel.com
This is the link to Amy’s TikTok page - over 20 million views for one video! Look up amyepohl on google
See my blog at http://www.gravitywheel.com
re: Blood From Stone
Fletcher:
Bessler was taking a little heat as he was calling himself a great mathematician but Wolff said he didn’t seem to profess a great talent (probably because Bessler was dabbling in geometry) upon meeting him. Also Wagner caught him in the math error of the wheel power being squared which I would suggest was the force itself not ultimate power of the wheel.
So a recap of what can be pulled out of that quote:
1) The principle once understood is simple and easy to understand. Meaning it must make intuitional sense.
2) It is deeply hidden in math but it is known in the early 1700. Meaning it wasn’t something magical the scientific community didn’t understand.
3) The math formulas head to an area where most people don’t work with in trying to make continuous motion.
4) That the principle may have more than one mechanical concept to achieve the math formulas computation.
5) The formulas must effortless stitch together, meaning no leaps of faith or fuzzy logic.
I am not so sure this is not purely a poor translated means of saying that better mechanical concepts of the wheel would probably arise. No different the progression of any invention in our time."(Page 64) ... , so I too am pleased to reflect that others, likewise through His goodness, possess a greater talent for analysing and describing, more artistically that I, this soon-to-be-revealed mystery ..."
Dang .. seems he thought others might be better able to analyse and drill down deeper than he could to describe his mechanical principle.
Bessler was taking a little heat as he was calling himself a great mathematician but Wolff said he didn’t seem to profess a great talent (probably because Bessler was dabbling in geometry) upon meeting him. Also Wagner caught him in the math error of the wheel power being squared which I would suggest was the force itself not ultimate power of the wheel.
So a recap of what can be pulled out of that quote:
1) The principle once understood is simple and easy to understand. Meaning it must make intuitional sense.
2) It is deeply hidden in math but it is known in the early 1700. Meaning it wasn’t something magical the scientific community didn’t understand.
3) The math formulas head to an area where most people don’t work with in trying to make continuous motion.
4) That the principle may have more than one mechanical concept to achieve the math formulas computation.
5) The formulas must effortless stitch together, meaning no leaps of faith or fuzzy logic.
What goes around, comes around.
re: Blood From Stone
....
Not everything I present is functional, but a surprise can't be completely ruled out.Greetings.
Re: re: Blood From Stone
I have no doubt that each and every one of us would be hugely disappointed if we found we had all been playing nicely together and digging in the wrong sandpit. History tells us that there is an extremely high probability that we have been. No one achieved a self-sustaining ever-lasting motion wheel before Bessler or 300 years since. Yet by his admission, he found it where everybody else had looked (the mind trap). IMO his simple mechanical principle looked like a OOB duck, quacked like a duck, waddled like a duck, but it wasn't a duck. It was a chimera ! That is it was an augmented OOB system that in and of itself had no torque and GPE advantage but whose function was re-purposed.daxwc wrote:Fletcher:I am not so sure this is not purely a poor translated means of saying that better mechanical concepts of the wheel would probably arise. No different the progression of any invention in our time."(Page 64) ... , so I too am pleased to reflect that others, likewise through His goodness, possess a greater talent for analysing and describing, more artistically that I, this soon-to-be-revealed mystery ..."
Dang .. seems he thought others might be better able to analyse and drill down deeper than he could to describe his mechanical principle.
Bessler was taking a little heat as he was calling himself a great mathematician but Wolff said he didn’t seem to profess a great talent (probably because Bessler was dabbling in geometry) upon meeting him. Also Wagner caught him in the math error of the wheel power being squared which I would suggest was the force itself not ultimate power of the wheel.
So a recap of what can be pulled out of that quote:
1) The principle once understood is simple and easy to understand. Meaning it must make intuitional sense.
2) It is deeply hidden in math but it is known in the early 1700. Meaning it wasn’t something magical the scientific community didn’t understand.
3) The math formulas head to an area where most people don’t work with in trying to make continuous motion.
4) That the principle may have more than one mechanical concept to achieve the math formulas computation.
5) The formulas must effortless stitch together, meaning no leaps of faith or fuzzy logic.
dax .. I just want to temporarily regroup your 5 observations .. and add a couple of validations.
1) The principle once understood is simple and easy to understand. Meaning it must make intuitional sense.
4) That the principle may have more than one mechanical concept to achieve the math formulas computation.
2) It is deeply hidden in math but it is known in the early 1700. Meaning it wasn’t something magical the scientific community didn’t understand.
3) The math formulas head to an area where most people don’t work with in trying to make continuous motion.
5) The formulas must effortless stitch together, meaning no leaps of faith or fuzzy logic.
You may be able to easily lay your hands on the info I'm about to relate from memory. I don't have an electronic copy of JC's books to search which makes looking for the detail laborious. And alto I used to have it on my laptop at one time, that went west when it was stolen years ago, and I never reconstructed my sources and index. I seem to remember some of it from Wagner's critiques and Bessler's DT response to Wagner IINM.
6) Bessler's mechanical principle could be seen by children playing in the street.
7) It was found in Nature.
Both these comments by Bessler point to simplicity and commonality of origin. N.B. the math may be complex.
Two children's games are favoured by me in this regard. One, being the spinning top game because of the obvious connection to the Toy's Page; and .. Two, being the tapping hoop game where children run beside a rolling hoop tapping it along. These games are still played in the street and in backyards and parks today. Both games can use a tapping stick to keep the top or hoop rotating.
I propose that the missing ingredient found in Nature is the Transmission of Waves thru a medium (a carrier of Momentum and Energy) seen in any body of water or air on a windy day, and which we are all familiar with, 300 years ago and now. And this I propose ties back to point 6) comment.
Enuff to think about for one day ..
-
MrVibrating
- Addict

- Posts: 2879
- Joined: Sat Jul 31, 2010 12:19 am
- Location: W3
New idea:
• drop a weight, using its descent to spin up a passively-expanding MoI
I've run preliminary tests already using a 'T' bar, like the Kassel pendulums - the opposing masses on the horizontal section are linked by a pantograph, syncing their radii, and stretching a spring between them as they slide outwards.
So it's basically some gravitating mass at fixed radius, plus some non-gravitating mass at variable radius, all attached to the same rigid T-member.
This is perched at -45°, and allowed to drop down through 90° of angle to 45°, where the sim stops.
Here's a very rough early example, just to illustrate the concept:
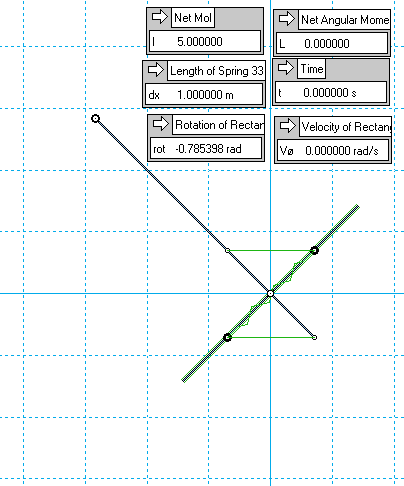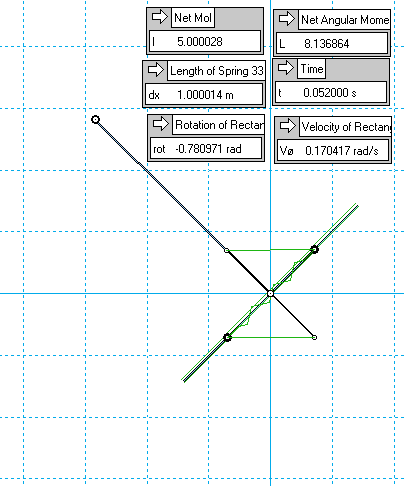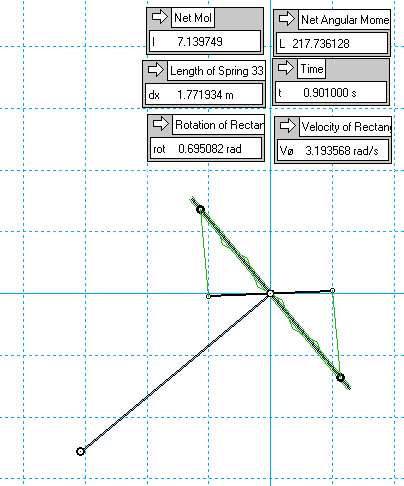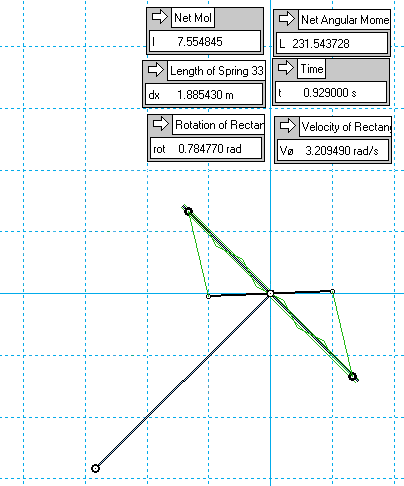
..if instead we perform the drop with the pantograph locked, so a fixed MoI, we net less momentum from gravity over the same 90° drop.
As before, the reason for this is the deceleration applied by the negative inertial torque from the expanding MoI, increasing the time spent gravitating.
Obviously, this is energy-neutral - whatever GPE is not converted into RKE is instead loaded into the spring.
But the focus of interest is what could happen next...
• Suppose that, with this time-boosted yield of momentum, we then immediately 'consolidate it' by striking it into a second angular inertia - say, a solid disc, of equal MoI at the moment of impact (7.55 kg-m^2 in the above example), using a simple inelastic collision.
This shares the momentum gain evenly between the T-section and the coaxial disc, leaving both rotating together at equal RPM.
As the weight starts to swing back upwards, the PE in the spring is released, retracting the MoI and so accelerating the weight back up, now reducing the time spent gravitating, and so giving less momentum back to gravity during the ascent, than was collected on the way down. A second collision again equalises the momentum and speed difference between the T-bar and wheel, and so the cycle repeats, stepping up in momentum and velocity - and thus RKE - each full cycle.
Let's see how far this one gets...
• drop a weight, using its descent to spin up a passively-expanding MoI
I've run preliminary tests already using a 'T' bar, like the Kassel pendulums - the opposing masses on the horizontal section are linked by a pantograph, syncing their radii, and stretching a spring between them as they slide outwards.
So it's basically some gravitating mass at fixed radius, plus some non-gravitating mass at variable radius, all attached to the same rigid T-member.
This is perched at -45°, and allowed to drop down through 90° of angle to 45°, where the sim stops.
Here's a very rough early example, just to illustrate the concept:

..if instead we perform the drop with the pantograph locked, so a fixed MoI, we net less momentum from gravity over the same 90° drop.
As before, the reason for this is the deceleration applied by the negative inertial torque from the expanding MoI, increasing the time spent gravitating.
Obviously, this is energy-neutral - whatever GPE is not converted into RKE is instead loaded into the spring.
But the focus of interest is what could happen next...
• Suppose that, with this time-boosted yield of momentum, we then immediately 'consolidate it' by striking it into a second angular inertia - say, a solid disc, of equal MoI at the moment of impact (7.55 kg-m^2 in the above example), using a simple inelastic collision.
This shares the momentum gain evenly between the T-section and the coaxial disc, leaving both rotating together at equal RPM.
As the weight starts to swing back upwards, the PE in the spring is released, retracting the MoI and so accelerating the weight back up, now reducing the time spent gravitating, and so giving less momentum back to gravity during the ascent, than was collected on the way down. A second collision again equalises the momentum and speed difference between the T-bar and wheel, and so the cycle repeats, stepping up in momentum and velocity - and thus RKE - each full cycle.
Let's see how far this one gets...
- Attachments
-
- droptest1.wm2d
- (17.8 KiB) Downloaded 59 times
-
Georg Künstler
- Devotee

- Posts: 1718
- Joined: Fri Nov 07, 2003 12:22 pm
- Location: Speyer, Germany
- Contact:
re: Blood From Stone
Hi MrVibrating,
I appreciate your work, great thingking and analysing,
but you always work with one System.
You need an energy excange from one System to an other. Interacting.
So you Need two Systems. a slower and a faster one, then swap.
With a single System you have no Chance.
I appreciate your work, great thingking and analysing,
but you always work with one System.
You need an energy excange from one System to an other. Interacting.
So you Need two Systems. a slower and a faster one, then swap.
With a single System you have no Chance.
Best regards
Georg
Georg
-
Georg Künstler
- Devotee

- Posts: 1718
- Joined: Fri Nov 07, 2003 12:22 pm
- Location: Speyer, Germany
- Contact:
re: Blood From Stone
Fletcher wrote:
The mathematic from nowadays is too complex so solve the riddle, the formula is there, but no one can build a model. Bessler has used a total simple way to calculate the torque of his wheel.
You Need a combination of knowledge.
One wheel of Bessler is "Impact driven" 8 Impacts per turn. An Impact is acting as a shock. Weights are shot upwards and creating torque in addition.
The function is a saw shape function.
if you like to build this function in you Simulation program, then you have to create 8 Independent moves. If you Simulation program can handle objects, create the object and place it in a carrier structure, 8 times.
The wheel will have, after the start always momentum.
the Impact is only there to arrange the weights.
the weights swing with their momentum ahead.
After the arrangement they produce torque.
the produced torque is then driving the wheel.
I propose that the missing ingredient found in Nature is the Transmission of Waves thru a medium (a carrier of Momentum and Energy) seen in any body of water or air on a windy day, and which we are all familiar with, 300 years ago and now. And this I propose ties back to point 6) comment.
The mathematic from nowadays is too complex so solve the riddle, the formula is there, but no one can build a model. Bessler has used a total simple way to calculate the torque of his wheel.
You Need a combination of knowledge.
One wheel of Bessler is "Impact driven" 8 Impacts per turn. An Impact is acting as a shock. Weights are shot upwards and creating torque in addition.
The function is a saw shape function.
if you like to build this function in you Simulation program, then you have to create 8 Independent moves. If you Simulation program can handle objects, create the object and place it in a carrier structure, 8 times.
The wheel will have, after the start always momentum.
the Impact is only there to arrange the weights.
the weights swing with their momentum ahead.
After the arrangement they produce torque.
the produced torque is then driving the wheel.
Best regards
Georg
Georg
- cloud camper
- Devotee

- Posts: 1083
- Joined: Tue Mar 15, 2011 12:20 am
Don't know how you would accomplish an inelastic collision but that would leave the T-section with half the momentum it started with, not enough to achieve a reset.MrVibrating wrote:New idea:
• drop a weight, using its descent to spin up a passively-expanding MoI
I've run preliminary tests already using a 'T' bar, like the Kassel pendulums - the opposing masses on the horizontal section are linked by a pantograph, syncing their radii, and stretching a spring between them as they slide outwards.
So it's basically some gravitating mass at fixed radius, plus some non-gravitating mass at variable radius, all attached to the same rigid T-member.
This is perched at -45°, and allowed to drop down through 90° of angle to 45°, where the sim stops.
Here's a very rough early example, just to illustrate the concept:
..if instead we perform the drop with the pantograph locked, so a fixed MoI, we net less momentum from gravity over the same 90° drop.
As before, the reason for this is the deceleration applied by the negative inertial torque from the expanding MoI, increasing the time spent gravitating.
Obviously, this is energy-neutral - whatever GPE is not converted into RKE is instead loaded into the spring.
But the focus of interest is what could happen next...
• Suppose that, with this time-boosted yield of momentum, we then immediately 'consolidate it' by striking it into a second angular inertia - say, a solid disc, of equal MoI at the moment of impact (7.55 kg-m^2 in the above example), using a simple inelastic collision.
This shares the momentum gain evenly between the T-section and the coaxial disc, leaving both rotating together at equal RPM.
As the weight starts to swing back upwards, the PE in the spring is released, retracting the MoI and so accelerating the weight back up, now reducing the time spent gravitating, and so giving less momentum back to gravity during the ascent, than was collected on the way down. A second collision again equalises the momentum and speed difference between the T-bar and wheel, and so the cycle repeats, stepping up in momentum and velocity - and thus RKE - each full cycle.
Let's see how far this one gets...
-
MrVibrating
- Addict

- Posts: 2879
- Joined: Sat Jul 31, 2010 12:19 am
- Location: W3
re: Blood From Stone
Okay here's the pendu-thing falling and striking a stopper on a wheel; first with the MoI locked:

..and then with the passively-widening MoI:

The sims pause just before the collision so you can see what's what, and then pause again at BDC when max momentum is reached.
As you can see, when the MoI is allowed to wander open, this slows the drop time, increasing the time spent gravitating and thus the momentum-from-gravity yeild.
This momentum is then banged into the wheel, at which point it's already been divvied out, so no taksie-backsies, it's ours, consolidated into the net system, a done deal.
However before progressing further, we can see an obvious bottleneck looming - if the objective of causing a CW / CCW angular momentum asymmetry is successful, the whole system's going to gain angular velocity...
..which in turn is going to raise the CF acting on these variable-MoI masses! Obviously, this means they're going to get stuck out at max radius, because we won't have sufficient energy in the spring to pull them back in, if the spring tension's optimised for this initial low speed.
What we'd need to do is raise the spring constant in step with the rising system RPM, so that CF force was only ever just strong enough to pull the masses out against the spring, loading it with the PE we need to pull the MoI back in post-collision..
Now, i'm not saying that's impossible, but it sounds like a bitch to engineer. There has to be a better solution...
...which there is, fortunately.
In the following demo, we have two identical flywheels, made from spring-loaded masses on radial slides.
As the flywheels spin up, the masses are pulled outwards by the growing CF, against the stiff springs.
One flywheel is left alone, the other's mounted to a wheel that's also spinning up:

...and we get this interesting result - quite unintuitively, the angular velocity of the wheel has no effect on the CF forces acting on the flywheel! Mounted and unmounted variants appear to be subject to identical CF forces!
This means that instead of mounting the crossbars coaxially, we should use axes orbiting the center! Then our per-cycle input energy and momentum yield should remain constant, irrespective of the wheel's rising RPM!
So, next up i'll try mounting two opposing crossbars, at mid-radius either side of the axle, and intersecting the center.
On the left, descending side, the weight lever will be allowed to drop, as its accompanying MoI increases, slowing its fall and so increasing its drop time and resulting momentum yield..
On the right, ascending side, the opposite weight lever will also be allowed to fall, while its MoI decreases, using only the same sprung tension gathered from the left-side drop. This should reduce its drop time, and thus the momentum yield.
Hopefully this should pan out to leave us with excess CCW net system momentum.
That's the plan anyway.. no apparently insurmountable issues thus far. If we quickly review our OU checklist, we can already tick the main boxes:
• accumulate 'reactionless' momentum (as from a momentum asymmetry) - more testing required on the current config but in principle it looks promising
• a constant momentum yield per cycle, despite rising RPM's - looks good here too, gravity's a uniform acceleration, not speed-dependent, and as shown above, the CF acting on an orbiting axis is purely a function of its intrinsic angular velocity, completely uncoupled from any orbital CF acting on that axis itself. In other words, the lever weights should gain exactly the same momentum each drop, irrespective of the rising system RPM's
• a constant input energy per cycle (ie. constant input energy for constant change in momentum per cycle), regardless of system RPM - obviously, GPE's not speed-dependent either, and again, the CF workload is also not RPM-dependent, hence no reason for input energy to square up with rising system velocity
..what more is there? That's basically the mechanical-OU spec-sheet right there, we've got a good hand here..
Only thing bothering me is the one-way wheels; B. suggested they ran on "completely different principles" to the bi-directional designs - different implementations of the same fundamental momentum asymmetry, surely - however we have to consider the issue of that static torque, that can only have been OB torque...
..and then, what of the ascending weight on the other side? Can't be counter-balanced against gravity, can't be any static advantage from a momentum asymmetry, so is it already lifted, or going to be lifted once rotation commences, or what? Either way, an internal PE store is implied. Springs or summink (that, or more weights).
The first issue that springs to mind however is that if the key to garnering more momentum from gravity on descent compared to ascent is this variation in MoI, then why rely on passive MoI variation during the drop - why not spend a little PE extending the MoI before dropping, hence further optimising the momentum yield?
But then you realise "why not just drop the weight as OB mass, ostensibly as B's one-way wheels were doing"? Think about it - if the trick is maximising angular inertia during descent, then the net system has much higher inertia that a single crossbar's varying MoI; it's rinsing the maximum possible momentum-from-gravity, by dropping it as slowly as possible given the available system mass / inertia..
..which would imply that the active exploit in the one-way wheels was actually a quick lift; ie. dropping the masses as OB weights on the descending side of the wheel, thus torquing up the net system with the max-possible momentum-from-gravity, and then reducing the MoI of the rising weight levers, to minmise their change in momentum-to-gravity.
That seems somewhat consistent anyway.. maybe we should be looking closer at the inverse trick, of cutting momentum lost to gravity whilst rising..? OB drop to BDC, then quick-lift with a shrinking MoI on the rising crossbars..?
Summink to fink about innit..

..and then with the passively-widening MoI:

The sims pause just before the collision so you can see what's what, and then pause again at BDC when max momentum is reached.
As you can see, when the MoI is allowed to wander open, this slows the drop time, increasing the time spent gravitating and thus the momentum-from-gravity yeild.
This momentum is then banged into the wheel, at which point it's already been divvied out, so no taksie-backsies, it's ours, consolidated into the net system, a done deal.
However before progressing further, we can see an obvious bottleneck looming - if the objective of causing a CW / CCW angular momentum asymmetry is successful, the whole system's going to gain angular velocity...
..which in turn is going to raise the CF acting on these variable-MoI masses! Obviously, this means they're going to get stuck out at max radius, because we won't have sufficient energy in the spring to pull them back in, if the spring tension's optimised for this initial low speed.
What we'd need to do is raise the spring constant in step with the rising system RPM, so that CF force was only ever just strong enough to pull the masses out against the spring, loading it with the PE we need to pull the MoI back in post-collision..
Now, i'm not saying that's impossible, but it sounds like a bitch to engineer. There has to be a better solution...
...which there is, fortunately.
In the following demo, we have two identical flywheels, made from spring-loaded masses on radial slides.
As the flywheels spin up, the masses are pulled outwards by the growing CF, against the stiff springs.
One flywheel is left alone, the other's mounted to a wheel that's also spinning up:

...and we get this interesting result - quite unintuitively, the angular velocity of the wheel has no effect on the CF forces acting on the flywheel! Mounted and unmounted variants appear to be subject to identical CF forces!
This means that instead of mounting the crossbars coaxially, we should use axes orbiting the center! Then our per-cycle input energy and momentum yield should remain constant, irrespective of the wheel's rising RPM!
So, next up i'll try mounting two opposing crossbars, at mid-radius either side of the axle, and intersecting the center.
On the left, descending side, the weight lever will be allowed to drop, as its accompanying MoI increases, slowing its fall and so increasing its drop time and resulting momentum yield..
On the right, ascending side, the opposite weight lever will also be allowed to fall, while its MoI decreases, using only the same sprung tension gathered from the left-side drop. This should reduce its drop time, and thus the momentum yield.
Hopefully this should pan out to leave us with excess CCW net system momentum.
That's the plan anyway.. no apparently insurmountable issues thus far. If we quickly review our OU checklist, we can already tick the main boxes:
• accumulate 'reactionless' momentum (as from a momentum asymmetry) - more testing required on the current config but in principle it looks promising
• a constant momentum yield per cycle, despite rising RPM's - looks good here too, gravity's a uniform acceleration, not speed-dependent, and as shown above, the CF acting on an orbiting axis is purely a function of its intrinsic angular velocity, completely uncoupled from any orbital CF acting on that axis itself. In other words, the lever weights should gain exactly the same momentum each drop, irrespective of the rising system RPM's
• a constant input energy per cycle (ie. constant input energy for constant change in momentum per cycle), regardless of system RPM - obviously, GPE's not speed-dependent either, and again, the CF workload is also not RPM-dependent, hence no reason for input energy to square up with rising system velocity
..what more is there? That's basically the mechanical-OU spec-sheet right there, we've got a good hand here..
Only thing bothering me is the one-way wheels; B. suggested they ran on "completely different principles" to the bi-directional designs - different implementations of the same fundamental momentum asymmetry, surely - however we have to consider the issue of that static torque, that can only have been OB torque...
..and then, what of the ascending weight on the other side? Can't be counter-balanced against gravity, can't be any static advantage from a momentum asymmetry, so is it already lifted, or going to be lifted once rotation commences, or what? Either way, an internal PE store is implied. Springs or summink (that, or more weights).
The first issue that springs to mind however is that if the key to garnering more momentum from gravity on descent compared to ascent is this variation in MoI, then why rely on passive MoI variation during the drop - why not spend a little PE extending the MoI before dropping, hence further optimising the momentum yield?
But then you realise "why not just drop the weight as OB mass, ostensibly as B's one-way wheels were doing"? Think about it - if the trick is maximising angular inertia during descent, then the net system has much higher inertia that a single crossbar's varying MoI; it's rinsing the maximum possible momentum-from-gravity, by dropping it as slowly as possible given the available system mass / inertia..
..which would imply that the active exploit in the one-way wheels was actually a quick lift; ie. dropping the masses as OB weights on the descending side of the wheel, thus torquing up the net system with the max-possible momentum-from-gravity, and then reducing the MoI of the rising weight levers, to minmise their change in momentum-to-gravity.
That seems somewhat consistent anyway.. maybe we should be looking closer at the inverse trick, of cutting momentum lost to gravity whilst rising..? OB drop to BDC, then quick-lift with a shrinking MoI on the rising crossbars..?
Summink to fink about innit..
-
MrVibrating
- Addict

- Posts: 2879
- Joined: Sat Jul 31, 2010 12:19 am
- Location: W3
An 'inelastic collision' is basically a thud, as opposed to a boing.cloud camper wrote: Don't know how you would accomplish an inelastic collision but that would leave the T-section with half the momentum it started with, not enough to achieve a reset.
Momentum is momentum, inertia times velocity, and not the potential to perform work (energy), so "resetting" is simply a case of whether or not we can perform a closed-loop cycle that gains momentum, irregardless of the energy cost. Because CoM is not supposed to be energy-dependent.
Again, the objective is to accumulate excess momentum from summing consecutive asymmetric inertial interactions, at fixed (ie. speed-invariant) energy cost and momentum yield per cycle.
So in short, we want an interaction that adds a fixed amount of momentum to the system each cycle, for a fixed energy cost, in spite of the rising net system RPM's. That breaks CoE. Because CoE is CoM-dependent.
Until one understands that last point, nothing i'm doing is going to make much sense i'm afraid - the KE gain resulting from a momentum asymmetry can only be anticipated mathematically; there is no 'magic lever' to look at to provide a visual reference for the principle of advantage: rather, the exploit is accelerating mass up to a given KE by using less energy than that standard KE value. Essentially, a way of getting more oomph from your PE. Classic example - accelerate two 1 kg masses up to 10 m/s, and hence a KE value of 100 J, by performing ten discrete 1 m/s accelerations costing 1 J each. Hence, an input energy of 10 J, for an output of 100 J. Where'd i pluck those numbers from? p=mV and ke=½mV², two 1 kg masses and any effective, cyclic, asymmetric momentum exchange.
So there simply is no way to represent that kind of advantage as a visual mechanical apparatus.. it's a preponderance of angular momentum of one sign over the other.
If your rate of change of momentum for a given weight is different between rising and falling over equal height, then that closed-loop trajectory gains or loses momentum to or from gravity. It may cost energy to do this. It could cost shed-loads. That's fine, though, provided the per-cycle efficiency (how much momentum we get for how much energy) remains constant despite rising RPMs.
With these conditions met, there is some threshold of RPM's below which we're under-unity, and above which we're over.
Examine for yourself the dependency of CoE upon CoM and this'll all start to make a lot more sense...
