Spring energy not conserved in rotating system.

[broli]

We all know when figure skaters pull in their arms while rotating they will spin faster.

Imagine a wheel with a weight on it attached to a compressed spring in such a way that when the spring releases the weight goes inwards (towards the center of the wheel).



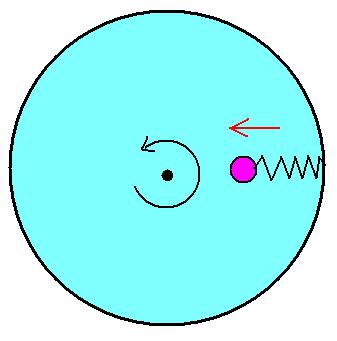
Now if the wheel is spun and at some point we release the spring. And for convenience sake let's assume the centrifugal force is much weaker than the spring force. The weight goes inwards and we see the wheel speed up just like the figure skater.

Now this is all interesting. But I found out that there's something strange going on when doing this. If you assume energy conservation is correct then you would assume that energy from the spring's decompression went in to the wheel. But when you use some common formulas you would not find energy conservation or even an energy gain. No, this system will magically suck energy out without giving it back.

A lot of people have been working with this but I have seen noone using the so called textbooks to show that energy is not conserved.

Of course this is the last thing we want. But this is interesting nonetheless? Here you have a closed system without any air, friction...losses that is losing energy.

This is all based on the conservation of rotational momentum. If you want math behind it I can make a presentation.

Edit: I just realized I forgot to account for something! The energy is not directly lost put put into another form which I have not thought of the whole day long. Maybe someone can spot it.

[Michael]

Well the ball has linear velocity ( kinetic energy ) that when forced to a tighter radius will cause the wheel to speed up, so that there energy is conserved. There is something interesting here though. The force from the spring will also cause the wheel to move backwards ( counter force ), to the direction of where the spring is applying it's force. Now if the wheels axle is anchored to the earth, since the earths mass and inertia is so large, this counter force won't be noticed ( but that is where the "missing" energy goes ). However if the axle was anchored to something smaller and movable, then it would be possible to create a linear movement of the whole object, if the springs release and weights inward movement was much faster than the weight and wheels rotation. A feat that is generally believed to be impossible to do, yet obviously very simple.

[broli]

Michael the thing I forgot to account for was the radial kinetic energy. The spring accelerates the mass inwards and thus this has a kinetic energy to it so I'm sure that if I incorporated that it would count up to be right.

But you just suggested something very interesting. You suggest using the reaction force that is other doing not much if the wheel was anchored.

This reaction force can be used linearly like you said. At the 3 o clock position the spring quickly decompresses to its maximum and locks up meanwhile the wheel will move to the right. Then while everything is locked up the wheel turn 180° where the process reverses. Now the locking mechanism is releases at 9 o'clock and the spring pull the wheel again to the right and locks up again when it's fully compressed. And turns another 180° where it gets released again and the process repeats.

This reaction force then can do work! I will think about this extensively.

[Fletcher]

Try that it wm broli with no air resistance - start it at 3 o'cl & lock the ball & tensioned spring [I like to use a small rod which can act like a latch to release or catch using the time function e.g. t<2.0 or t>4.0 - if you want you can use an IF statement e.g. IF(t<2,1,0] or IF(t<2,0,IF(t>6,0,1))

Now put a fake force on the ball to represent system frictional losses & adjust it till it swings to say 8 o'cl [with ball locked all the time] - repeat but let the latch go & a second latch catch the ball at a closer radius some time later - see how high it turns - use measure velocity [rpm] & measure angle of rotation so you can see at a glance how high it gets.

This is also the basis of how a child swings on a swing i.e. by lifting their CoM at various times changing the radius of the CoM [that would make an interesting model to work on] - you should see an increase in the height attained by the ball due to CoAM.

N.B. if you attach the ball to a sliding pivot radial it makes things easier - also some interesting things happen if the acceleration force gets larger & larger & the amount of acceleration force becomes important rather than the time it acts, IINM.

[Michael]

Hi Broli. Yes when I said linear motion I was refering to the balls kinetic energy. I should have said rotational kinetic energy. The released springs energy is stored in the earth, unless the axle isn't fixed to the earth.

[BAR]

I dont understand how surplus energy is created here? When you measure the total energy of a system related to volume, (which is the analogy of the skater) simply collapsing the volume increases velocity but not total energy, energy is conserved less friction. The momentum must travel a shorter distance per unit time which is the same total energy but higher velocity.