Hi one and all,
Straight off may I suggest that you print this if possible (has to be worth 4 sheets of copy) and more importantly MAKE the simple models described as you will stand little chance of appreciating the theory without them.
Please construct the following; Take a circle, divide into 6 pie segments, cut them out. Rebuild hinging one against the other adding a 7th segment.
Place it flat on a surface and it will look like this:
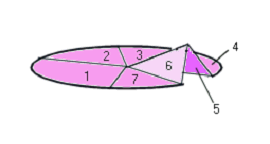
You will see that this toy has a Jacobs Ladder type action, that segment 5 in falling flat will shift 6, in turn dragging 7 down and away from its flat position.
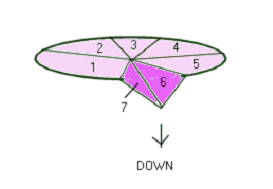
This action repeats right around, 3 segments moving at a time and at each rev. the action of each segment is reversed, i.e. next time around 6 & 7 will point up.
Hold the thing upright and the kink resides at the bottom of course and you'll see that it is a balanced kink across 3 segments. Turn the thing and see how 3 segments constantly remain at the base, constantly snaking back and forth as you turn. Note in particular the central one of these 3 segments as it swings back and forth across the axle's perpendicular...
Imagine this annoyingly floppy toy being held firm, ACTING around an axle. In principle it would sit as already described, excess weight under the axle but what if you give it a slight nudge in any direction ?
Common sense suggests that it would turn for a bit, snake for a bit and then come to rest once again, weight under the axle. But as common sense may be entirely inappropriate for this particular puzzle then I ask you to think very carefully before allowing assumptions to cloud your view.
I only possess schoolboy physics and it didn't cover this one so I can't make any claims. I can only imagine. Feel free to set me straight.
As already mentioned there is a 7th weight (segment) constantly moving across the axle line. The 7th weight is actually a stream of segments which each move through the axle one by one, always in the same direction but swinging back and forth. Across and away from your nose, across and towards your nose if you catch my drift.
I know nothing of pendulums especially ones tied up like this but is it possible that gravity is seeing 7 weights, the axle is seeing less and the excess is being fed to drive the swing ? What situation would we have if once set in motion then all the action takes place horizontal to the axle. Four weights connected to the axle and over to one side against three moving, falling and unconnected weights on the other side ? Like me you will probably find it difficult to imagine this thing, hopefully now in front of you, actually attached to and acting upon an axle
If so then at this point please now construct the following.
Take 3 more circles of the same size (purely convenience). Divide into 6 again cutting out 3 alternate segments to leave 3 still connected at the centre. The point at which they connect should be as small as practical. Repeat this with the second circle leaving you with a total of six loose segments. Divide the 3rd circle into six segments and cut these out to give a total of 12 loose segments now. Returning to the 2 `joined at a point` circles, in each of the 6 spaces fix in 2 segments. You should end up with 2 anvils like this
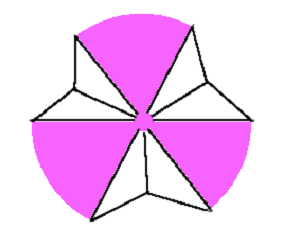
Turn it over, flat segments down and it looks awfully like Bessler's diagram However, place one on a surface, flat side up as shown. Over this place the 7 segment floppy thing such that the kink fits into one of the 3 available dips in the anvil.
Place the 2nd anvil on top, flat side down and align the 2 anvils so that all flat sides are opposed by dips and visa versa. Fix in this position.
You should now have a framework, the 2 anvils, in which the floppy thing can freely move in the action already outlined.
OK its only a rough toy and it doesn't move freely but it allows you to get the point yes ? This frame will attach the weights, the PM itself to the axle, to a C of G so that gravity can suss it out and work on it.
Try and imagine some precisely engineered version with heavy segments and anvils made from some strong/light polymer. Imagine also this important addition. Each flat section of each anvil should have a central peg protruding from it and all 7 segments of the floppy should have a central hole. In this way all flat segments are locked onto anvil pegs whilst the snaking 3 are not.
You may notice that the floppy can be formed from any size of circle. It can be made much larger than the anvils for instance and still it will fit in and be held by them.. Still it will perform the same action. The floppy can be huge compared to it's cage so long as it's cage is strong enough to cope. From this you might further note that you could employ small segments each with a weight connected like so;
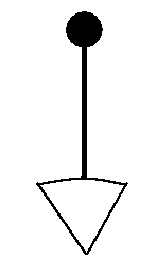
Like this you would have a small cage with long arms extending from it's centre. The longer the arms and the larger the weight they hold then the more power, as Bessler said. At all times we have 4 weights spread around the top and 3 out of place and snaking at the bottom.
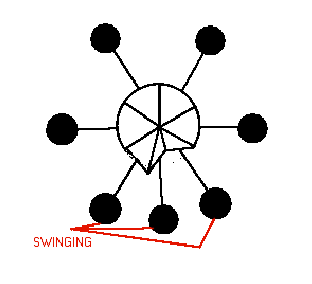
- Bottom weight, left is out towards you
- Bottom centre lies dead centre and straight down
- Bottom, right is in away from you
My gut feeling is maybe but if it IS something then something is not quite right but perhaps it's that common sense thing again. What do you reckon ?
You might also wish to muse over the following.
- Anvils/blows ?
- The flail (pendulum) ?
- Cat slinks ?
- Tail wags ?
- Peacocks tail front/side ?
- Normal Rim ?
- Left/right, both directions ?
- Theory of excess weight ?
- Principle of perpetual movement ?
- Weights are PM ?
- One or more applied vertical perhaps horizontal to axle ? (know there's some dispute re translation)
- A Jacob's ladder of sorts but acting in a parallel (watch it carefully) fashion akin to the other toy on THAT page ?
- Plate 85 page 27 in J Cs book. Cheeky, smiley chappie on a pendulum giving it a sneaky kick ?
- The six segment anvil diagram plus 1 = 7. That's 1 = 7 ?
- And finally, although I offer no theory at this point, 4 balls and 2 back to back Prince Sabu bowls appears to promise the possibility of achieving the same excess weight/pendulum action as the above, only better/smarter.
All the best,
Gill Simo/Glastonbury/uk. (11.8.2003)